分散と共分散の考え方と計算の手順

回帰分析において、避けて通れない用語として、分散、共分散があります。とりわけ、共分散についてはイメージがつかみづらいので、実例をみながら考えます。

分散と標準偏差

はじめに分散について振り返ります。例としてA,B２つのグループ各5人にテストを行い、得点が次の通りであったとします。グループ毎の傾向を比較するうえで、全体で均してみてどれくらいの得点という平均だけでなく、全体で均してみてどれくらい平均からはばらついているかを示す分散、標準偏差を計算する必要があります。分散、標準偏差は次の手順で計算します。

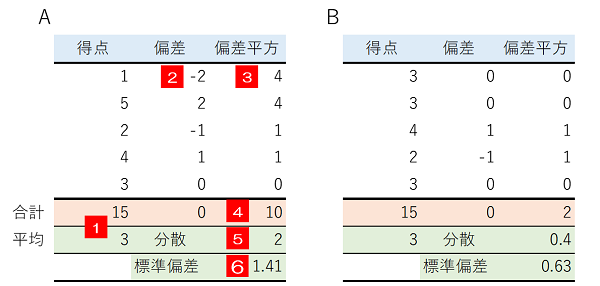
この結果、AグループとBグループの得点を比較すると、平均はいずれも3で同じですが、分散はAグループが2、Bグループが0.4となり、Aのばらつきの方が大きいことがわかります。

共分散の計算

共分散は広告件数と新規顧客数のように2つの量の関係を測ります。$x$と$y$の各データにつき偏差（値$-$平均）の積を計算し、合計したものを積和といいます。さらに、積和をデータの個数nで割って共分散を求めます。

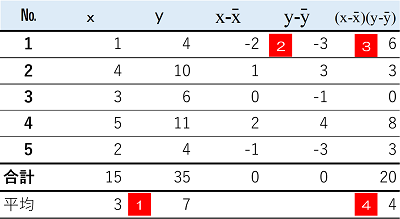
計算方法はこれだけですが、共分散は何をあらわしているのかイメージしづらい概念なので、例を挙げて詳しく見てみます。

共分散の意味

$x$が増加するに従い$y$も増加する正の相関

$x$と$y$の関係を表にします。

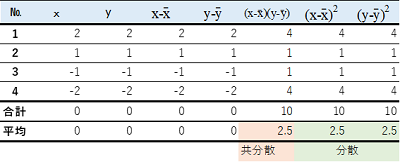
表だけではイメージがつかめないのでグラフにします。

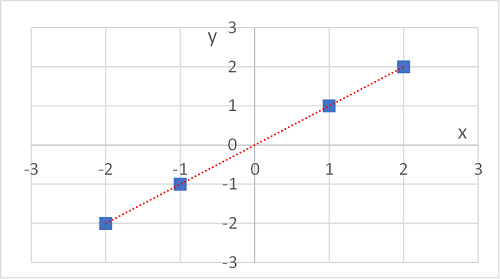
$x$が増加するに従い、$y$も増加しています。また、しかも、ここでの例は4つの点がきれいに直線の上に並んでいます。このような関係を正の相関関係といい、共分散の値はプラスになります。なおかつ、共分散の値は$x$や$y$の分散と同じ大きさになっているので強い相関関係になるといえます。

$x$が増加するに従い$y$が減少する負の相関

次に、逆の例を見てみます。

グラフにすると次の通りになります。

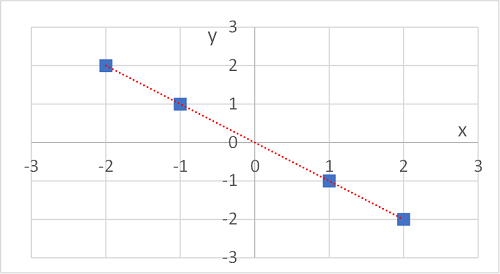
こんどは反対に$x$が増加するに従い、$y$が減少しています。しかも、やはり$x$と$y$がきれいに一直線に並んでいます。このような関係を負の相関関係といい、共分散は$x$や$y$の分散をマイナスした値になります。

相関がみられない場合

もう一つ、こんなケースも考えられます。

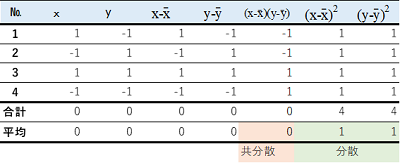
図にすると次の通りです。

回帰直線を引くにも引きようがなく、$x$と$y$の間に相関関係を見ることができません。このような場合、（$x$の偏差）×（$y$の偏差）は+と-が打ち消し合い、共分散は0になります。

現実的な数値

これまで非常に極端な例を挙げてきましたが、最後に少し現実的な例を挙げます。

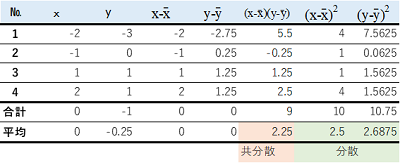
グラフにすると次の通りです。

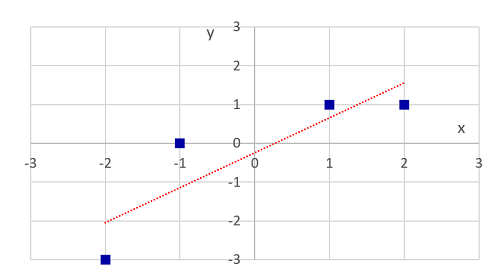
$x$と$y$は正の相関関係にはありますが、キレイに直線上に並んでいません。この場合には共分散はプラスになりますが、$x$や$y$の分散に比べると小さな値となっています。このことから共分散は、次のような数字であると考えられます。

$x$と$y$の分散が大きれば、共分散はそれにつられて大きくなります。しかし、$x$と$y$の間に相関関係が小さいと、その分だけ共分散は小さくなります。つまり共分散は、2つの量がどれくらい相関関係を持ちながらばらついているかということをあらわしています。

まとめ

分散や共分散の計算方法についてご紹介しました。ここでの計算は一度平均を求めてから、再度各データと平均との差を求めるなど複雑です。実はもっと簡易な方法で計算することができます。

共分散の考え方を使うと、回帰直線の傾きと切片（回帰係数）を簡単に計算することができます。