回帰直線の傾き、切片の計算方法を直感的に理解する

広告数と新規顧客数のような二つの変数の相関関係を見るときに、散布図から $x$ と$y$ の関係を読み取って目分量で回帰直線を引くことができます。人によって結果が少しずつ異なるなど不都合が生じます。そこで数学的な根拠を持って計算し、誰がやっても同じ結果になるようにする方法はないか探ってみます。

一次式による近似曲線の表示

一次式による回帰分析は、確率変数$x$の値から$y$の値を予測するとき、$y= \alpha+\beta x$の関係にあると考えます。$\beta$は傾きといい、xが1増えると$y$がいくつ増えるかを表します。$\alpha$は切片といい、$x$が0のとき$y$がいくらか、つまり散布図にしたときに回帰直線と$y$軸と交わる点（交点）をいいます。散布図から回帰直線を目分量で引く代わりに数式として表現するためにはどうすればよいでしょうか。

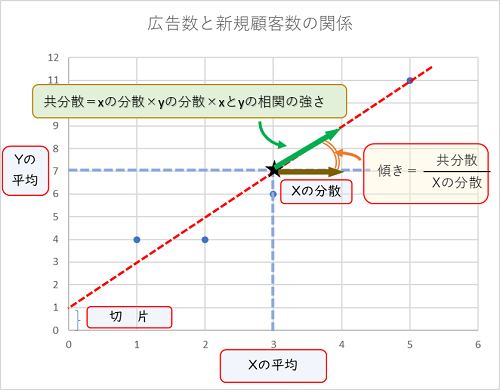
まず、$x$、$y$、それぞれの平均の組み合わせの点に注目します。回帰直線は散布図に打った点のちょうど中間を突っ切ると考えると、$x$、$y$の平均の点を通ることが考えられます。次に、回帰直線の傾き$\beta$を考えます。$x$の分散は$x$が均してみてどの程度ばらついているかを表します。一方、$x$と$y$の共分散は次の式で計算します。

になるので、共分散を$x$の分散で割ると、$x$が1だけ平均からばらつくと、$y$がどれだけ$X$と相関を持ちながらばらついていくか、つまり傾き表します。そこで、回帰直線では傾きを次のように計算します。

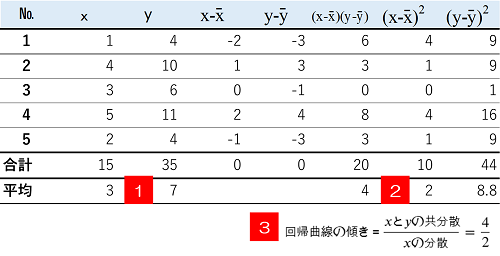
これで、$y=\alpha+2x$となりました。最後に式は$x$、$y$の平均の点（x=3,y=7）を通るので、代入すると$\alpha$=1になります。実際に散布図に回帰直線を式の通り描いてみると結果は良好のようです。

また、ここでは傾きを、式：[共分散÷$x$の分散]で計算しましたが、共分散は[積和÷データ数]、分散は[偏差平方和÷データ数] なので分母と分子にデータ数を掛けて[積和÷データ数]で計算した方が手間を省くことができます。

以上のことをまとめると次の通りになります。

まとめ

回帰直線の計算方法がイメージできたと思います。数式化することで、だれが計算しても同じ結果になることは非常に大きなメリットです。

しかしここでの方法は、数学的にはかなり大雑把です。数学的にしっかりと証明したい場合には偏微分という技術を使う必要があります。

回帰直線の式を計算することができたが、本当に実務に耐えるものなのかはさらに検証する必要があります。