相関係数をPythonで計算する

Pythonを使ってサンプルデータから相関係数の予測値の計算をします。はじめに、NumPyを使って積和や偏差平方和を手順通りに計算します。

計算の内容

次の表を測定値のデータとして使います。説明変数を$x$、目的変数を$y$として、相関係数を求めます。

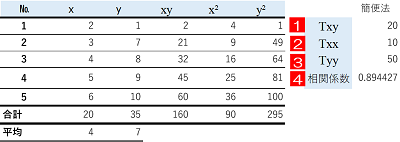
相関係数の計算
相関係数の計算

詳しい手順は次の通りです。

１　積和$T_{xy}=x$×$y$の合計$-(x$の合計×$y$の合計/データ数)＝$160-(20×35/5)＝20$
２　偏差平方和$T_{xx}=x^2$の合計$-(x$の合計$^2$/データ数)＝$90-(20^2/5)＝10$
３　偏差平方和$T_{yy}=y^2$の合計$-(y$の合計$^2$/データ数)＝$295-(35^2/5)＝50$
４　相関係数＝決定係数の計算　$T_{xy}/(\sqrt{T_{xx}}\sqrt{T_{yy}})=20/(\sqrt{10}×\sqrt{50})$

なお、全体を通して使う変数は次の通りです。

用語 変数 意　　　　味
xのリスト x 説明変数xの配列NumPyで計算するのでndarray形式で定義
yのリスト y 目的変数yの配列、ndarray形式で定義
偏差平方和 T_{xx},T_{yy} 回帰分析ではT_{xx}と表現される。平方根した数値が分散
積和 T_{xy} 回帰分析ではT_{xy}と表現される。平方根して数値が共分散
相関係数 r 2つの変数の相関の強さを表す。$T_{xy}/\sqrt{(T_{xx}×T_{yy})}$

NumPyで計算

手順通りの計算

はじめに関数を使わず手順通り計算します。NumPyで使うためndarrayで$x$,$y$を定義し、簡便法を使い積和、偏差平方和を求めたのち、決定係数を計算し、さらにその平方根を求めることで相関係数になります。

# NumPyを使って簡易法により計算
  1. import numpy as np
  2. x=np.array([2,3,4,5,6])
  3. y=np.array([1,7,8,9,10])
  4. n=len(x)
# NumPyで相関係数を計算する
  1. t_xy=sum(x*y)-(1/n)*sum(x)*sum(y)
  2. t_xx=sum(x**2)-(1/n)*sum(x)**2
  3. t_yy=sum(y**2)-(1/n)*sum(y)**2
  4. r2=t_xy/(np.sqrt(t_xx))*(np.sqrt(t_yy))
  5. print(' 相関係数=',r)

結果は次の通りです。

相関係数= 0.8944271909999159

NumPyモジュールのcorrcoef関数による方法

次にNumPyモジュールのcorrcoef関数を使います。

corrcoef関数で相関係数を計算する
  1. print(np.corrcoef(x,y))
  2. r=np.corrcoef(x,y)[0][1]
  3. print(' 相関係数=',r)

corrcoef関数は配列を返します。相関係数をプログラムの中で使うためにはnp.corrcoef(x,y)[0][1]で相関係数を求める必要があります。

[[1.         0.89442719]
 [0.89442719 1.        ]]
 相関係数= 0.8944271909999157

まとめ

統計学のテキストでは相関係数がよくつかわれますが、corrcoef関数は高度な分析を前提としているので相関係数を直接求めることができません。実は、相関係数とよく似たもので決定係数というものがあります。これらのモジュールでは決定係数を中心に分析をすることを前提としているようです。