回帰分析の特徴を直感的にとらえる
回帰分析では、例えば広告の件数から新規顧客数を予測する場合に、その関係を$新規顧客数=傾き×広告件数+切片$という式であらわし、実際の値と比較して差を分析します。ここで、傾きや切片、差異の間にはさまざまな興味深い関係がみられます。これらの関係は、さらに高度なことを学ぶ上で大切なことです。
各数値の確認
まず、表とその中で登場する数値についてまとめます。

| № | 記号 | 内容 |
|---|---|---|
| A | $x$ | 説明変数の実際の測定値 |
| B | $y$ | 目的変数の実際の測定値 |
| C | $x-\bar{x}$ | $x$の偏差 平均値との差異 |
| D | $(x-\bar{x})^2$ | $x$の偏差の2乗 合計が$x$の偏差平方和、データ数で割ると分散 |
| E | $y-\bar{y}$ | $y$の偏差 平均値との差異 |
| F | ($y-\bar{y})^2$ | $y$の偏差の2乗 合計が$y$の偏差平方和、データ数で割ると分散 |
| G | $(x-\bar{x̄})(y-\bar{y})$ | $x$の偏差と$y$の偏差の積 合計が積和、データ数で割ると共分散 |
| H | $\hat{y}$ | $y$の予測値$\hat{y}$ 傾き:2+切片:1 |
| I | $\hat{y}-\bar{y}$ | $y$の予測値と平均の差 |
| J | $(\hat{y}-\bar{y})^2$ | $y$の予測値と平均の差の2乗 |
| K | $e$ | 予測値$\hat{y}$と測定値$y$の差 残差 |
| L | $e^2$ | 残差の2乗 |
| M | $xe$ | $x$と残差の積和 |
| N | $(x-\bar{x})e$ | $x$の偏差と残差の積和 |
| O | $\hat{y}e$ | $y$の予測値と残差の積和 |
| P | $(\hat{y}-\bar{y})e$ | $y$の偏差と残差の積和 |
この表から、次のことがわかります。
回帰直線と平均の関係
回帰直線と平均の関係をまとめます。
予測値の平均と観測値の平均が等しい
$y$の測定値(B)と、回帰直線の式から求めた予測値(H)の平均はともに7で等しくなっています。もともと回帰分析は、$x$,$y$の測定値の平均を起点に分析するので直感的に納得できると思います。
回帰直線は$x$と$y$の平均値の座標、点($x$,$y$)を通る
式:$y=2x-1$に$x$=4を代入すると$y$=7となり、確かに平均の座標(4,7)は回帰直線上にあります。このことも、回帰分析は$x$,$y$の測定値の平均を軸に分析することから納得できると思います。
残差の分析
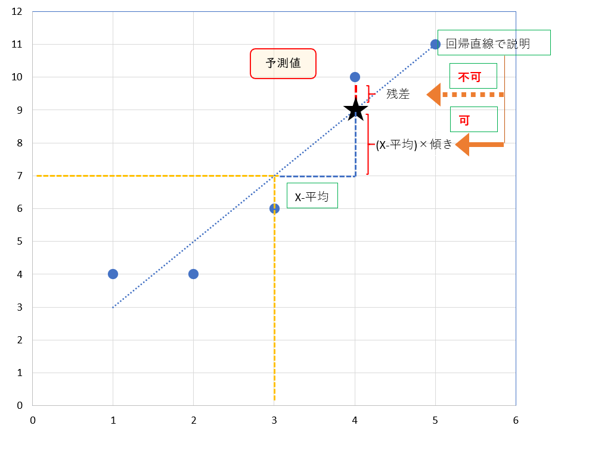
測定値と予測値の間の差である残差には、非常に面白い特徴があります。
残差の合計は0である
表においても残差の合計 (k) は0になっています。回帰直線を引くときに、各データの点のカタマリを上下に均等に分けるように引きました。このため、残差は回帰直線をはさんで上下にバランスよく散らばっていると考えると、プラスマイナスが打ち消され合計が0になります。
説明変数$x$および目的変数$y$と残差の相関係数はいずれも0である
イメージしづらいですが大切な関係です。表において、(M)では説明変数$x$と残差$e$の積を合計していますが、0になっています。また、(O)では目的変数$y$と残差$e$の積を合計していますがこれも0になっています。
回帰直線はその式によって$y$の分散のうち説明できる回帰の部分を最大限にし、逆に説明できない残差の部分が最小になるように傾きの値を決めました。このため、$y$の分散のうち$x$の値から説明できない部分が残差に集約されていると考えられます。したがって、説明変数$x$と残差には相関関係が全く、両者の相関係数は0になると考えられます。
次に、$y$の予測値(測定値ではない)は$x$から$y=\beta x+\alpha$の式で単純に計算されるので、残差と$x$の相関関係が0であれば、$y$の予測値との相関係数が0であると考えられます。
回帰直線のあてはまりの良さを測る決定係数
$y$のデータ一つ一つの偏差は、回帰直線によって説明できる部分と説明できない部分に分けられます。そこで、それぞれの数値の合計のバランスを見ることにより、回帰直線のあてはまりの良さを測ることができます。しかし、単純な合計では残差の合計が0になってしまいうまくいかないので、それぞれの数値を2乗したものを比べます。
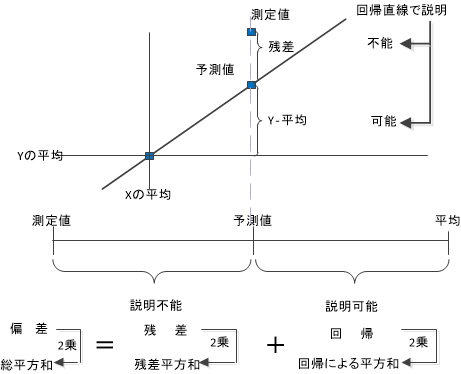
式の左辺の偏差2乗の合計は偏差平方和です。いっぽう、右辺の残差の2乗は残差平方和、回帰の2乗は回帰による平方和といわれ、両者の合計は偏差平方和と等しくなります。
ここで現れる数値を使い、回帰直線がどの程度、当てはまりが良いかを測る指標として決定係数を計算します。 決定係数は、総分散に対して回帰直線により説明できる回帰による平方和の比率であり、大きいほど回帰直線のあてはまりが良いことになります。ところで決定係数を計算するうえで偏差や残差の2乗を使ったので、元に戻す意味で決定係数を平方根にします。すると結果は0.8となり、相関係数と一致します。つまり、決定係数は相関係数の2乗になります。このため$R^2$というような書き方をすることがあります。ただ、注意事項として、負の相関の場合には相関係数はマイナスになりますが、決定係数は2乗されるのでプラスに符号が変わります。 最後に、決定係数についての用語をまとめておきます。 回帰分析の特徴について、おおざっぱに見てきました。次はこれらの関係を数式で確認します。決定係数
用語
英字
記号
意味
総平方和
SST
total sum of squares
$S_{y}$
目的変数$y$の分散
$y_{i}-\bar{y}$(yの測定値-yの平均)
回帰による平方和
SSR
regression sum of squares
$S_{R}$
総平方和のうち回帰曲線により説明可能な部分
$\hat{y}-\bar{y}$(yの測定値-yの平均)
残差平方和
SSE
error sum of squares
$S_{e}$
総平方和のうち回帰曲線では説明できない部分
$y_{i}-\hat{y}$(yの測定値-yの平均)
まとめ