回帰係数の期待値と分散、標準誤差の計算
回帰係数の分散を計算する必要性
回帰分析において、新規顧客数を予測することを例とします。まず、新規顧客数に最も影響を与えるのは広告の件数であると考え、これまでのデータを分析します。このとき予測したい新規顧客件数を目的変数といい、あらかじめわかっている広告件数を説明変数といい、次のような関係式を想定します。
新規顧客数=傾き×広告件数+切片
傾きと切片(併せて回帰係数といいます)はあくまでサンプルのデータの中では最も当てはまりの良い数値であるにすぎず、その説明変数が精度よく予測できているという保証はありません。したがって回帰直線の結果に何ら検討を加えることなく、予測された新規顧客件数をもとに商品を仕入れたり人を雇ったりするのは危険なことです。回帰分析の結果を実務に役立てる際には、求めた傾きや切片がどれくらいばらつくのかを統計的に計算し、予測と異なった場合の対応も考えておく必要があるわけです。
母集団とサンプル
回帰分析において、すべてのデータ(母集団)を調べつくすことは費用の問題から不可能な場合がほとんどです。例えば、広告件数から目的関数である新規顧客数を予測する場合も、分析のためにすべてのすべて広告件数を何度も試すようなことはできず、限られたサンプルから予測するほかありません。このため、回帰分析で予測した傾きや切片には、母集団の真の傾きや切片との間に差が生じるのはやむを得ないことです。たまたま取ったサンプルが母集団を代表するようなデータであればよいのですが、確率的には低いにしても、神様のイタズラによってかなり特異なデータばかりを選んでしまうこともありえます。そこで、このばらつきの具合を統計的に計算することができれば、例えばサンプルから計算した傾きが10であった場合、次のような検討ができます。
- 母集団の傾きも10である可能性が一番高いけれど、実際には9.8~10.2の範囲である確率が68%、裏を返せば100回のうち32回は9.8より小さかったり10.2よりも大きかったりすることも想定する必要がある。
- 本当は相関関係が無いのに、たまたま取ったサンプルで計算したら傾きが10となったのか、それとも本当に傾きが10に近くなるような相関関係があるのか?
このような分析ができると、「これくらいの誤差が出るのは想定内だ」、「もっと違う説明変数を使って分析しよう」という判断ができるようになります。
式の傾きの期待値
回帰直線の式の傾きの期待値、つまり母集団の式の傾きがいくつであると期待されるかを考えます。この場合、母集団のすべてを調べることはできないので、サンプルから最小二乗法により計算した傾きを期待値とするよりほかはありません。例えば、サンプルのデータの傾きが10だとすると、母集団の傾きがピッタリ10であることはないとしても、大体10をはさんでそんなに離れていない数字であることが期待されるわけです。同様に、切片についても、サンプルから計算した切片を期待値とするほかはありません。
傾きの分散
母集団の誤差
サンプルから予測した回帰直線の傾きがどれくらいばらつくかを計算します。その前に、母集団において説明変数と目的変数の関係がきれいに一直線に並んでいる状況(つまり相関係数が1や-1)を考えます。この場合、測定ミスがなければ、抽出したサンプルもきれいに一直線に並ぶはずです。母集団のデータがきれいに直線状に並んでいたら、どの組み合わせのサンプルを取り出しても、データが回帰直線から外れることは考えられないためです。しかし、現実にはこのようなことは極めてまれで、新顧客数は広告件数と強い相関関係にあったとしても、広告以外のルートで訪れるお客さんもいれば、広告が鼻につくとほかの店に行ってしまう人もいて、母集団の中で回帰直線を引いても、その直線からはずれるデータがいくつかあるはずです。この実際の値と回帰直線で計算した値の差異を誤差といいます(サンプルの測定値と予測値との差異である残差とは異なります)。そして、母集団の誤差が大きければ大きいほど、それにつられて取り出したサンプルで計算した回帰直線の傾きのばらつきも大きくなります。

回帰直線の傾きの分散
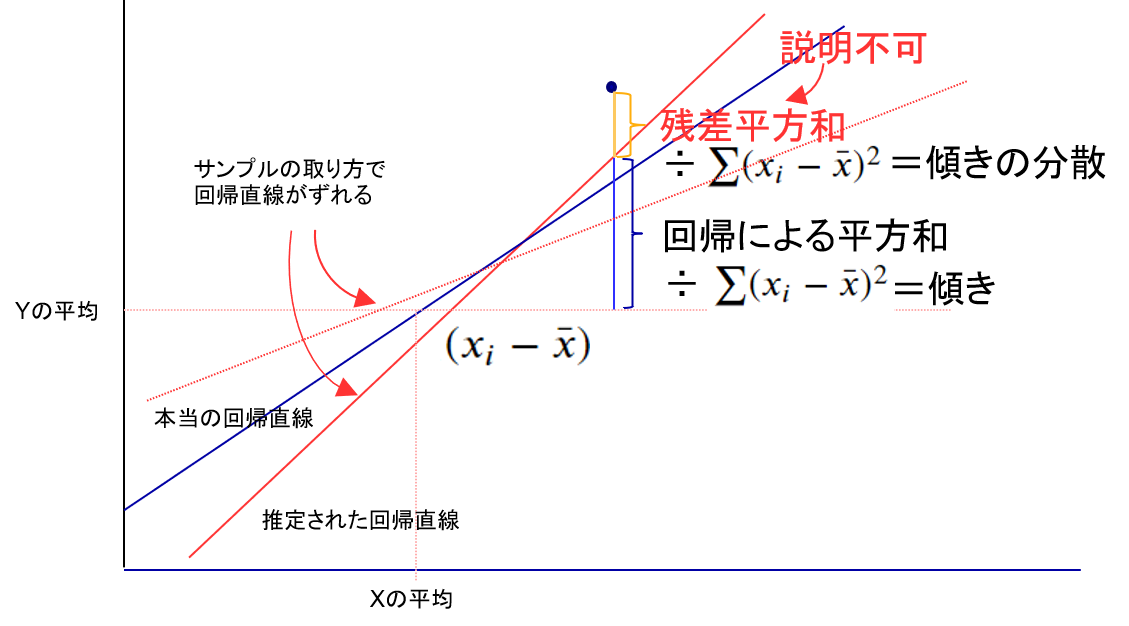
誤差とサンプルの傾きの分散の関係を考えます。母集団のすべてのデータから、最小二乗法により計算した回帰直線(青い実線)を想定します。もちろん、これがどのような式かは神様にしかわかりません。
母集団のデータから回帰直線上にないものを取り出して、その測定値を(広告件数,新規顧客数)=(X,Y)とします。$Y$と$Y$の平均$\bar(Y)$の差異の2乗が$Y$の偏差平方和ですが、これは、回帰直線によって説明可能な「回帰による平方和」と、「説明不能な残差平方和」に分けることができます。
ところで、回帰直線の傾きは「回帰による平方和」を説明変数$X$の偏差平方和で割ることにより計算することができます(正確には傾きの2乗になります)。一方「説明不能な残差平方和」は、$X$とは何ら相関がない部分で、回帰直線の傾きのばらつきの原因となっています。この数値をデータ数で割ることにより「説明不能な残差平方和」の分散を計算することができ、さらに、傾きの計算と同じように説明変数$X$の偏差平方和で割ることで、傾きのばらつき具合を計算することができます。実際には、「説明不能な残差平方和」は誤差の2乗をもとに計算しているので、元に戻す意味でこの数値の平方根を取ります。分散の平方根を標準偏差といいますが、ここでは誤差を対象としているので、特別な用語として標準誤差と呼ばれています。
残差による誤差の推定
これまで、回帰直線の傾きの分散は母集団の誤差から計算できることを示しましたが、我々は母集団のすべてのデータを調べることは通常できないので、サンプルから推測する方法を考えます。実は、誤差の分散はサンプルの残差の分散の値とほぼ等しくなることがわかっています。
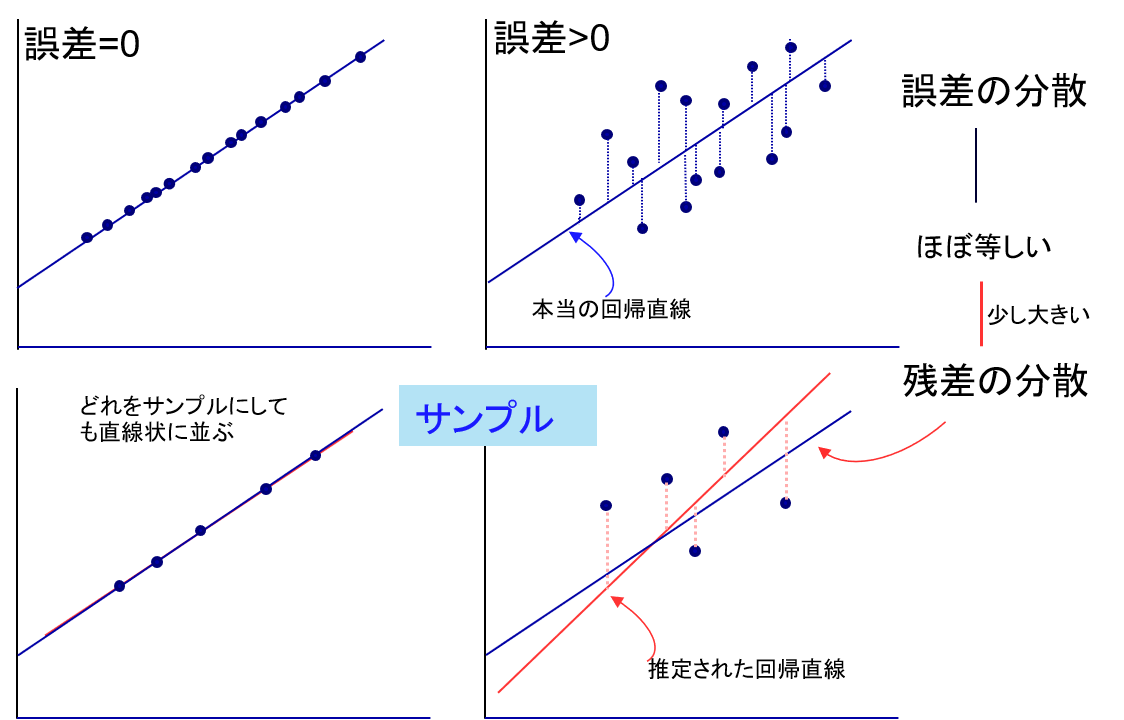
図表3のように、母集団の誤差がなければサンプルにおいても残差が発生することはありません。また、誤差がある場合は、その大きさがそのまま残差に反映され、等しくなると考えるのは自然です。ただ、厳密にいうと、推定された回帰直線から計算した残差は本当の回帰直線と比べると母集団の誤差よりも過小に計算される傾向にあります。
母集団からサンプルを抜き出して、そこから回帰直線を推定しています。この直線はサンプルのYの値である残差は、本当の回帰直線との誤差より小さくなっているもの(赤い部分)もあれば、大きくなっているもの(緑の部分)もあります。そして全体的にみると、推定された回帰直線はサンプルから計算しているので、それに引きずられて、残差は小さくなりがちです。
詳しいことは数学的に証明する必要がありますが、通常は残差平方和をサンプル数$-2$で割ると残差の分散が誤差の分散の推定値として最も適した数値となります。
回帰直線の傾きの分散
このことから、回帰直線の傾きの期待値と分散は次の通りになります。また、データのバラツキについて評価をするときには分散の平方根である標準偏差を使います。同様に、傾きのばらつきに関する評価をするときも平方根した数値を使いますが、回帰分析の場合には誤差から計算するので、標準誤差といわれています。以上をまとめると次のようになります。また、通常、分散の平方根は標準偏差といわれますが、回帰分析の場合は標準誤差といいます。
傾きの期待値、分散、標準誤差
まとめ
イメージとして、回帰係数の予測値の期待値と分散を計算することができました。ただし、厳密には数式で証明する必要があります。