回帰分析の傾きの区間推定

回帰分析の区間推定の考え方

回帰分析で広告件数から新規顧客数を予測する場合、いろいろな広告件数で実験を繰り返して調べ上げることはできないので、手に入る限りのサンプルから計算せざるを得ません。例えばサンプルから計算した回帰直線の式の傾きの推定値が10であったとします。ここで本当の傾きは「大体10くらいであることが期待されます」というだけでは実務ではあまり役に立ちません。これに対して、正規分布や T 分布の考え方を使うと、分散（あるいはその平方根である標準偏差）が分かっていれば、「真の傾きは68パーセントの確率で10±0.2つまり9.8から10.2の間に収まる」というような推定をすることができます。このような考え方を区間推計といいます。

それでは、回帰分析に正規分布に関する区間推計の考え方を採り入れてみます。まず、正規分布について振り返ってみます。あるデータは、分散があらかじめわかっています。今、そのデータの平均値を推定したいとします。本来であればすべてのデータを調べ上げれば正確な平均を計算することができます。しかし、コストの関係からそれはできないとするとサンプルを取って、その平均を推定値とするしかありません。このとき、サンプルの平均の標準偏差は母集団の分散÷サンプル数の平方根になります。

母集団の分散（既知）　　20 サンプル数　5　　サンプルの平均　10

サンプルの平均の標準偏差　$\sqrt{20/5}=2$となるので、サンプルの平均は、

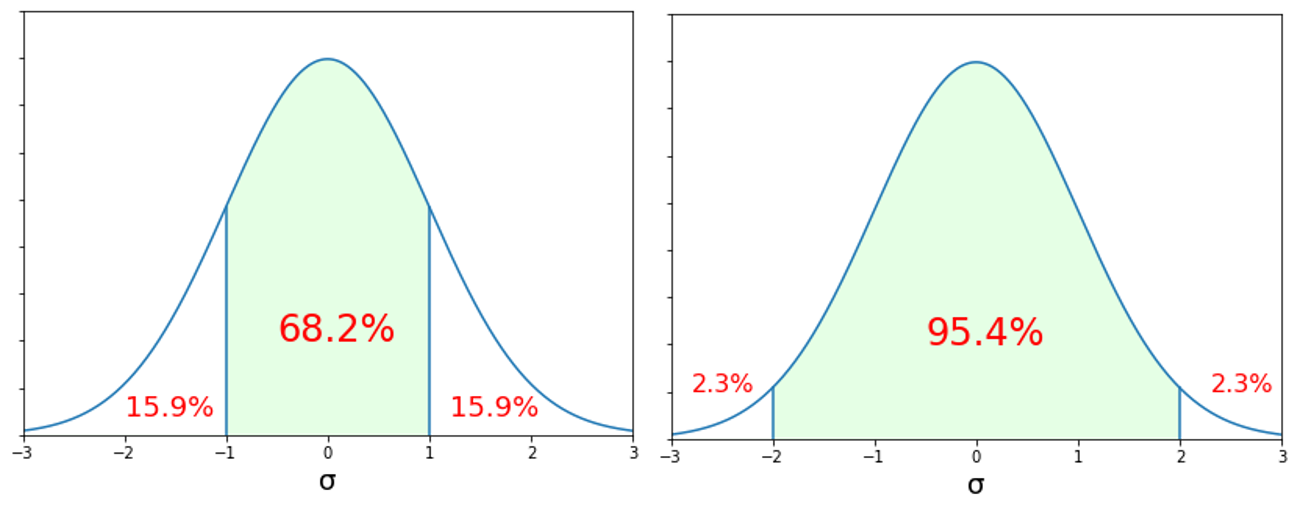
この場合、データの平均は$10\pm\sigma\times1=10\pm2$となり、8から12の間である確率が68.2%となります。また、12を超える確率と8を下回る確率はそれぞれ15.9%になります。さらに、範囲を広げて$10\pm\sigma\times2=10\pm4$となり、6から14の間である確率が95.4％になります。

ｔ検定による傾きの区間推定

ここで、正規分布を回帰分布にあてはめたくなりますが、正規分布の考え方は実は少し厳しい条件が付けられています。というのは母集団の分散があらかじめわかっている場合ということです。例えばもうすでに何年も同じように広告件数に対する新規顧客数が同じ分散で推移しているというような場合です。そして毎月回帰分析をすることにより例えば今月は広告件数に対して新規顧客数が少ないという場合にこれは偶然なのかそれとも広告以外の要素、例えばお店に対して悪い噂が立っているあるいはそもそも時代が変わってきて今のままの方法が時代に合わなくなっているかを検証するために使う場合にはこの方法で大丈夫です。

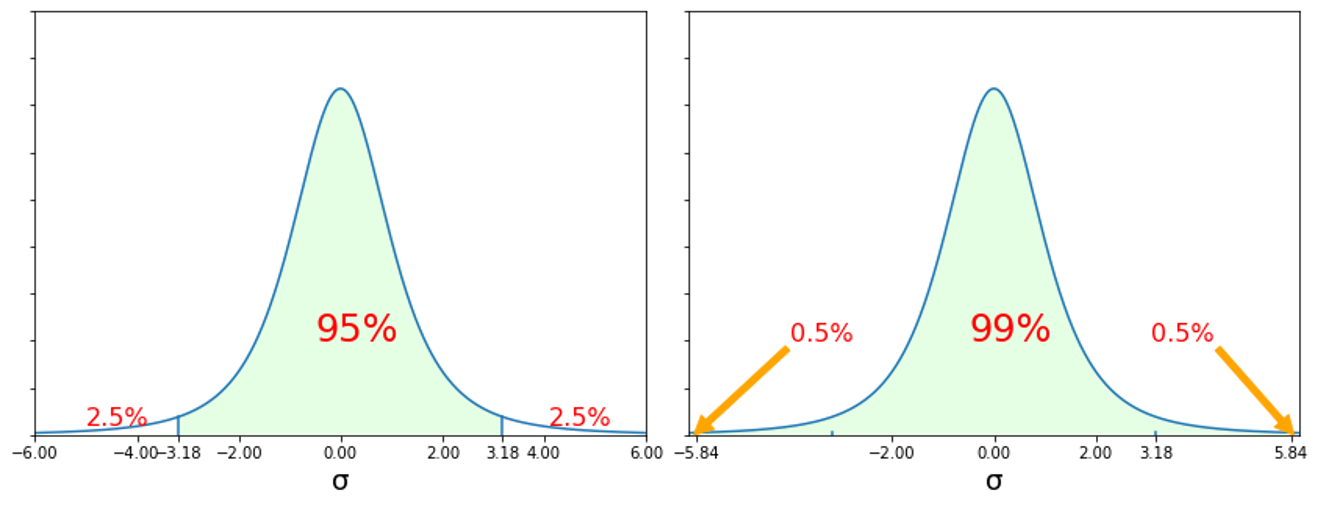
このように分散があらかじめわかっていることはまれなので、その場合にはt分布を使います。t分布は母集団の分散がわからないのでサンプルから計算した分散を使って計算します。このため、サンプルの数によって分布が変わってきます。説明変数が1つの回帰分析では自由度をサンプル数-2で計算します。

広告件数から新規顧客数を予測する場合、傾きがとても大切な要素になります。傾きの標準誤差は、

そこでサンプルから推測するしかありませんが、このときには残差平方和をデータ数から2を引いた数字で割って求めた値で近似することができます。2を引いた数字ということは残差平方和÷データ数で計算すると　は少し過小評価される傾向にあるので、これをただすためにデータ数-2とするとちょうどよくなります。

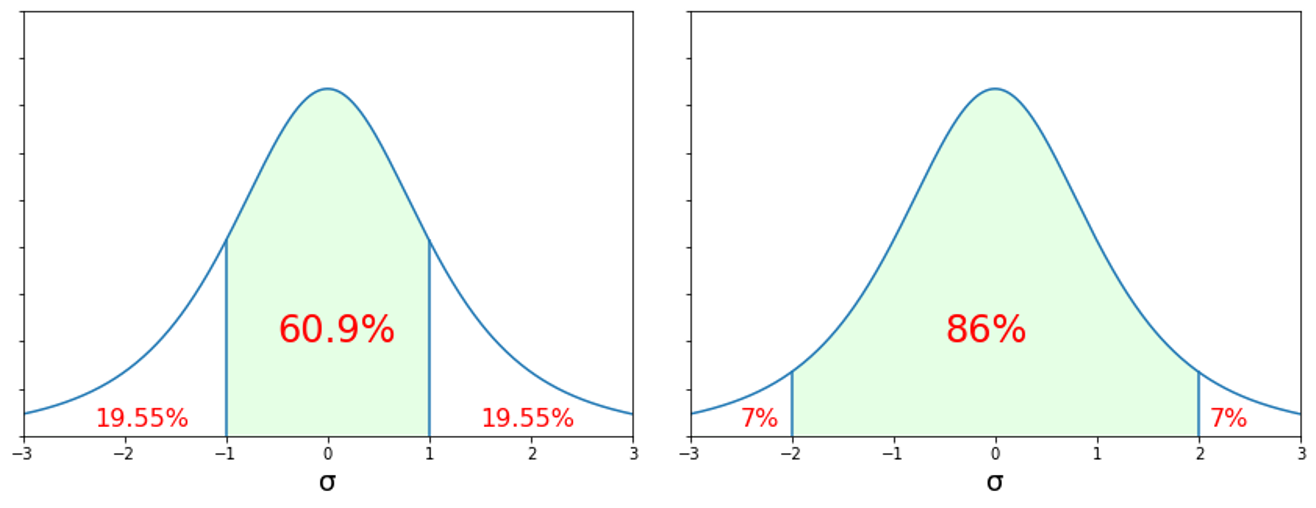
$\pm\sigma$を取ると60.9％となり、正規分布より幅が狭くなります。同様に$\pm2\times\sigma$の場合には86%となります。つまり、同じ範囲を考えてもはずれる確率が高くなります。

$\sigma$は母集団の分散なので

例えばサンプルから計算した傾きが2で標準偏差が0.2の場合1.8から2.2の範囲の中が68%1.6から2.4の範囲な96%というように計算することができるわけですこの1.8から2.2という範囲のことを信頼区間といい、その範囲に収まる確率が95%といった場合、この95%を信頼係数といます。

なお、自由度ごとのt分布と正規分布の比較は次の通りになります。

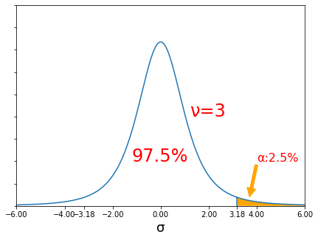
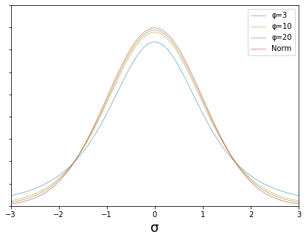
自由度が小さい（サンプル数が少ない）ほど、グラフの裾が長くなっています。つまり、同じ区間をとってもその区間の信頼度が下がってしまうこと示しています。逆に自由度が20になると正規分布にかなり近づいているように、自由度が大きくなるにしたがい正規分布に使づいていきます。

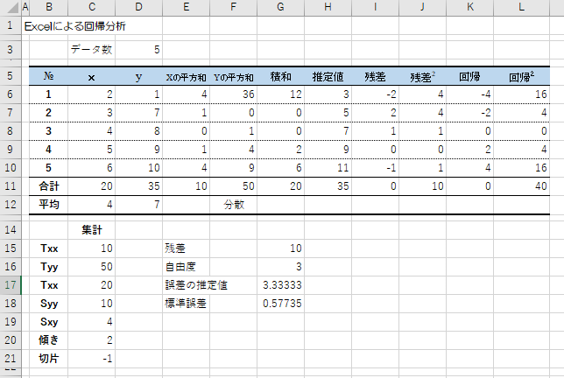
具体例による区間推定