統計学の基礎
平均値
学生の身長やテストの成績など、たくさんのデータの特徴を説明するために最もよく用いられるのが平均値です。平均値は各データの合計を求めて、データの数で割り算をすることにより計算することができます。ある試験で、クラス5人の得点が40,50,60,70,80点の場合、平均点は次にように計算して60点となります。
\begin{align} 平均 = \frac{40 + 50 + 60 + 70 +90}{n} = 60 \end{align}試験をすれば、その教科が得意な人、苦手な人がいるので、でっこみひっこみが生じます。このでっこみ引っ込みを均して、おしなべていくらかという代表的な値を平均と言います。この計算を少し数学っぽく表現すると次にようになります。
まず、統計の世界ではxの平均は$ \bar x $(エックスバー)といいます。つぎにデータの数がn個(nはnumber)あり、それぞれの値を$ \ n \ $個の数値$ \ x_1, x_2,\cdots,x_n $とします。このとき平均値は次のとおり計算します
\begin{align} \bar x = \frac{x_1 + x_2 + \cdots + x_n}{n} = \sum _{k=1} ^ n k \end{align}平均は英語ではaverage、meanといいます。
トリム平均値
平均値の計算で、データの数が少ないときに極端に大きな値や小さな値があると、それに引っ張られて平均点がデータの特徴を正しく表すことができなくなってしまいます。そこで、データの中から上下両極端のデータをいくつか取り除くように工夫する必要があります。
例えば、フィギュアスケートでは、最大9人の企業審判が、いくつかの項目ごとに-5から+までの11段階で採点し、それを平均して順位を決めます。このとき、他の協議に区レベルと審判の主観が入ってしまう恐れがあります。そこで、競技ごとの得点のうち、最も高い点数と低い点数を取り除いて、残った数字で平均点を計算するようにしています。
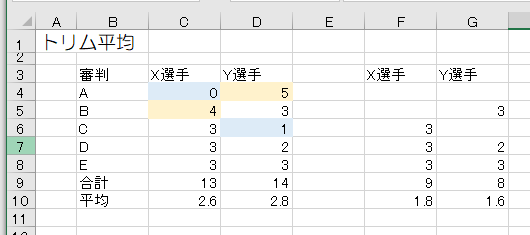
次のように、X選手とY選手をAからEの5人の審判が採点したとします。単純に平均するとY選手の方が高得点になります。しかし、よく見るとA審判以外はX選手の方が良い得点か同じ点数を付けています。そこで、それぞれから最も高い点数と低い点数を取り除いて、平均点を計算します。この結果X選手の方が高い得点になり、より実態にあった評価ができるようになることがあります。
平均以外の
平均値のほかにも、データの代表を示す値はいろいろあります。
中央値(median)
データを大きさの順番で並べたとき、ちょうど真ん中(中央)になる値が1つあれば、その値が中央値となります。もし、データの数が偶数であり、中央になる値が2つあれば2つの値の中間が中央値になります。中央値はメディアン(median)というようにいう場合もあります。
データが5つで、9,5,3,2,1であれば、中央値は3、データが6つで、10,9,5,3,2,1であれば、中央値は5と3の間を取って4になります。
最頻値(mode)
データの中で度数が最も多い値を最頻値といいます。最頻値は英語ではモードといいます。たとえば、データが6,5,4,4,4,3,2,1であれば、4が3つで一番多くなるので最頻値は4になります。