Pythonで取り扱うことができる整数の最大値

Pythonではどんなに大きな整数でも扱うことができる

「実践力を身につけるPythonの教科書」で、2の500乗を求める計算が紹介されていました。やってみると、紙と鉛筆でやれば一生かかるよう計算をPythonは図のとおりたちどころにやってのけます。

print(2 ** 500)

3273390607896141870013189696827599152216642046043064789483291368096133796404674554883270092325904157150886684127560071009217256545885393053328527589376

そこで、Pythonでは、いったいどれくらいの桁数の整数を扱うことができるのか調べてみました。結論からいうと、マシンの性能が許す範囲であれば、どんなに大きな整数でも扱うことができるようです。

Pythonの3系ではsysモジュールにmaxsizeという組み込み変数があり、Py_ssize_t′^の変数が取りうる最大値を示してくれます。Py_ssize_tのssizeとはSequencesizeの略で、リストなどの要素の数をもののようですが、よくわからないので後で調べてみようと思います。

#maxsize変数でy_ssize_t変数が取りうる最大値を求める
import sys
import math

x = sys.maxsize
print(x)
print(math.log2(x + 1))

2147483647
31.0

Windows32ビットOSでは2,147,483,647（2の31乗‐1）になります。これに対し、64ビットOSの場合は次のようになります。

9223372036854775807
63.0

64ビットなのに1桁少ない63乗というのは、プラスとマイナスがあるためだと思われます。それでも19桁というのは922京3372兆・・・という数字だけでもとんでもないことになります。しかし、これはあくまでもリストの要素数などの話なので、通常の計算であれば、前に紹介した通り、さらに大きな数字が扱えるというわけです。

エクセルとの比較

それでは我々がいつもお世話になっているエクセルではどうでしょうか？

マイクロソフトのホームページによると、有効桁数は10の15乗と書かれています。

セルA1に14桁で1番大きな数字999兆9999億9999万9999－1を入力し、列幅を広げた上で整数表示にします。これに対し、数字を1ずつ足し算していくと、おかしなことが起こります。

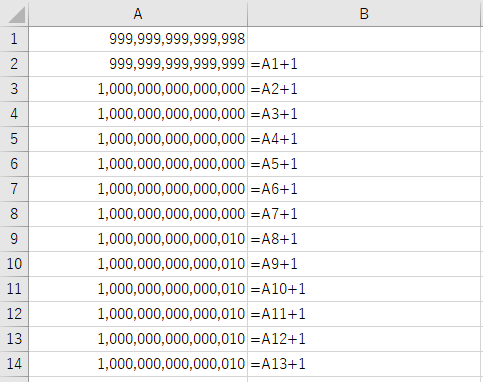
セルA3の1000兆ぴったりまでは良いのですが、それに1を加えても1000兆とおなじ数字が表示されます。そして1000兆6になった時点で1000兆10となり、整数部分を勝手に四捨五入してしまいます。（細かいことをいうと下1桁が5のときは切り下がっているので、JIS丸めによっているものと思います。）おそらく我が国の事務処理の分野で1000兆円を超える数字を扱うのは、財務省で国債の残高を管理している部門くらいだと思います。このような意味ではエクセルでも十分のような気がしますが、次のような計算をすると、下1桁は一目で1と分かるのに、計算結果の下1桁は0と明らかにおかしなことになります。

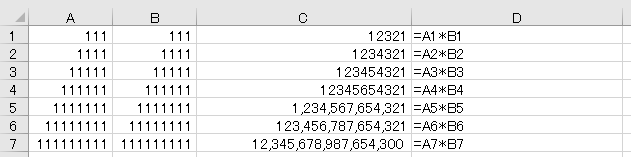
その点Pythonはいくらでも計算してくれます。

#print(111 * 111)
print(1111 * 1111)
print(11111 * 11111)
print(111111 * 111111)
print(1111111 * 1111111)
print(11111111 * 11111111)
print(111111111 * 111111111)
print(1111111111 * 1111111111)
print(11111111111 * 11111111111)
print(111111111111 * 111111111111)

12321
1234321
123454321
12345654321
1234567654321
123456787654321
12345678987654321
1234567900987654321
123456790120987654321
12345679012320987654321

この計算、8行より後はあまり面白い結果は出ませんが、Pythonの地味にすごいところを示してくれています。