2021年– date –

• 

  ある整数の約数に対するオイラー関数の和がある整数になる

• 

  Pythonで小数型の数値を2進数、さらには16進数に変換する

• 

  2進数での丸め処理をする関数

• 

  バーゼル問題と円周率

• 

  マチンの公式でどれくらいの精度で円周率を計算できるか？

• 

  円周率10万桁

• 

  $\tan \pi/4=1$から円周率を計算する

• 

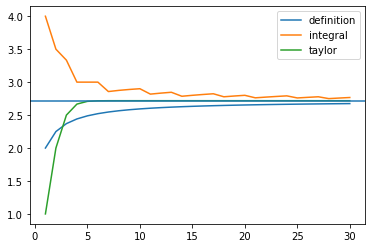
  Pythonでネイピア（Napier）数を計算する

• 

  Pythonで平方根を計算する

• 

  1/81が０.0123456790・・・というように循環する理由