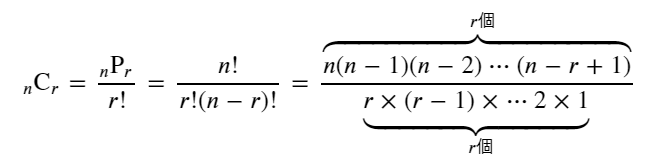2023年9月– date –

!python --version Python 3.7.16

リストの初期化 list_init = [[] for _ in range(4)] list_init[1].append('x') list_init [[], ['x'], [], []]

順列・組み合わせ 重複順列 r人をn個の部屋に分ける $_{n}\Pi_{r}=\underbrace{n\times{n}\times\cdots\times{n}}_{r個の積}=n^r$ 順列 $1\le x_i\le n,1\le x_j\le n,k_i\ne k_j,1\le i\lt j \le k$ $\displaystyle {}_n\mathrm{P}_r = \frac{n!}{(n-r)!}...

順列・組み合わせ 重複順列 (sequence with repetition) r人をn個の部屋に分ける $_{n}\Pi_{r}=\underbrace{n\times{n}\times\times{n}}_{r個の積}=n^r$ 順列の個数(permutation) $1\leqq x_1\ne x_2\ne\cdots \ne x_k \leqq n$ $\displaystyle {}_n\mathr...

きますが、k=pqが合成数の時には、$2^k - 1 = 2^{pq} - 1$ =$ (2^p-1)(2^{pq -p}+\cdots+2^{3p}+2^{2p}+2^p+1)$となり、 メルセンヌ素数に$2^{k-1}$を掛けた値が完全数になるのは次の計算ができるためです。 整数nが完全数であるため nの約数の合計:Sとす...