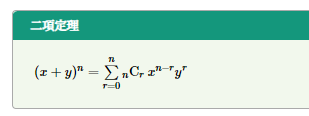ictsr4– Author –
-

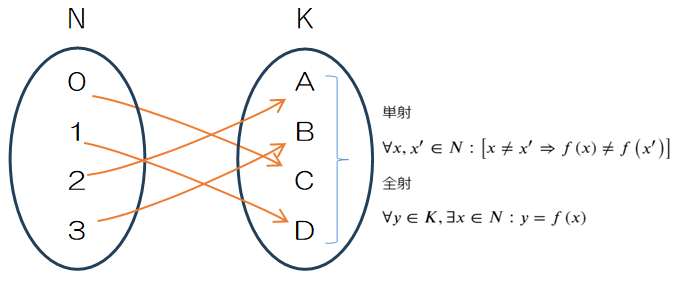
はじめに 写像について
順列・組み合わせなど場合の数の問題では、解答までの流れはおぼろげながら理解できるものの、全体像が今一つすっきりとしない、少し複雑な問題に出くわすと途方に暮れてしまう、こんなことがよくあります。良い方法はないかと模索しているうちに、写像と... -

第1種スターリング数の生成と多重のタプルの結合
第1種スターリング数を生成する関数を作成しました。 Pythonの標準パッケージ等にはにはベル数や第1種スターリング数を生成する関数がないので、自作するしかありません。その際にいろいろな方法で作成し、比べることにより答え合わせをする際に、多重の配... -

重複順列、順列と包除原理
重複順列についてご紹介します。 重複順列 -

組み合わせ
四則演算などPythonでの基本的な計算を取り上げました。練習問題はかなり面白いものが入って -

スターリング数
-

分割数
Pythonで小数、分数、n乗根を計算する https://ictsr4.com/info/p10130.html -

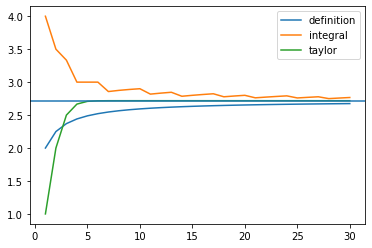
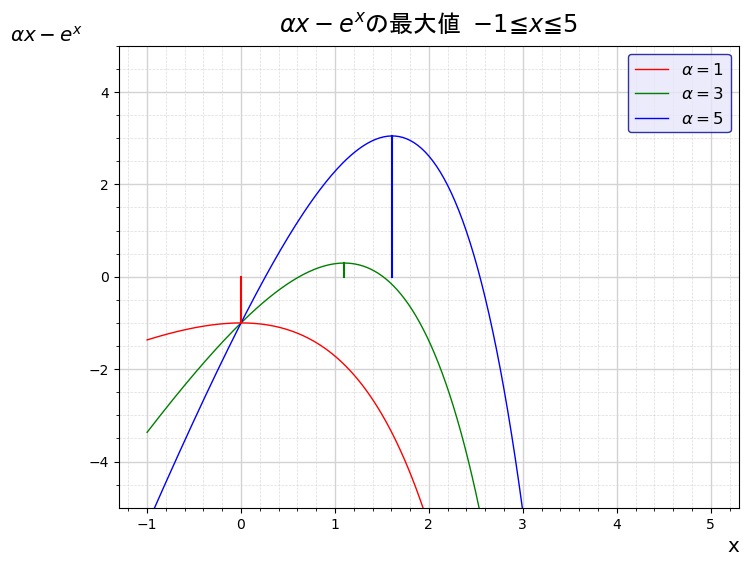
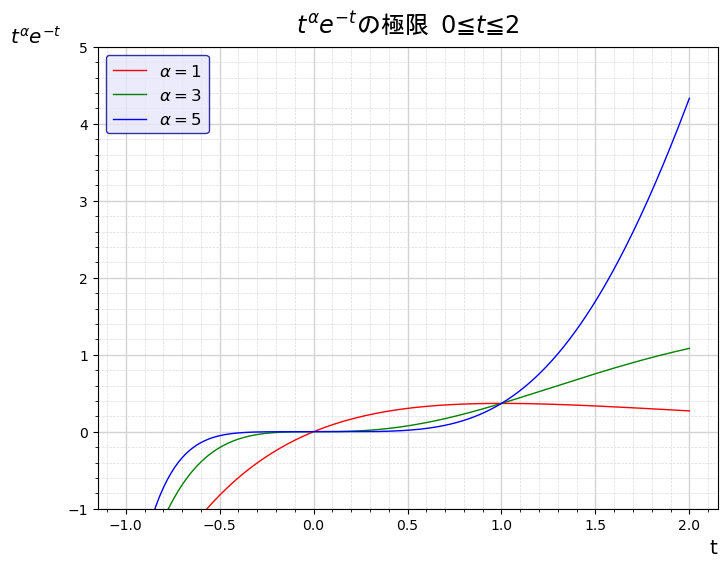
自然対数
自然対数 $\displaystyle e = \lim_{x\to \infty} \left(1+\frac{1}{x} \right)^{x}\sim2.718281828459045$ 「鮒、一鉢二鉢一鉢二鉢至極美味しい」という語呂合わせがあります。 マイナスの無限大について $t=-xとおくと$ $\displaystyle\lim_{x \rightarr... -

二項定理
二項定理について 二項定理の考え方やPythonのプログラムを説明しています。 https://ictsr4.com/info/p10160.html https://ictsr4.com/info/e10160.html -

おすすめ書籍
詳細!Python3入門ノート [ 大重美幸 ] ggggg -

Python環境
!python --version Python 3.7.16