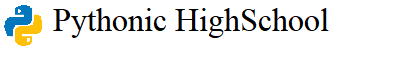写像の定義とその応用

写像

写像の定義と写像ではないもの

写像とは

写像とは集合 $X$、集合 $Y$ において、集合 $X$ のそれぞれの要素に対して集合 $Y$ の要素がただ一つ対応する規則のことです。それではFigure 0.1をもとに、写像の概念を探っていきましょう。

集合 $X$ を写像の定義域（domain）、集合 $Y$ を終域（codomain）と呼びます。

定義域は集合 $X$、終域は集合 $Y$ のように英大文字を使うのが一般的ですが、 $N$ 、$K$ のように $X$ 、$Y$ 以外の文字を使う場合もあります。写像を表す記号には関数を意味するfunctionの頭文字である$f$を使い、$f:X\longrightarrow Y$ と表記します。

例えば、 １ のような $X=\{1, 2, 3 , 4\}$ 、$Y=\{1, 4, 9, 16\}$ として、$y=x^2$ という対応を考えます。どの $x$ に対しても、 $y$ が 1 つ決まるので写像になります。

次に ２ のような $X=\{1, 2, 3 , -3\}$ 、 $Y=\{1, 4, 9, 16\}$ とし、写像 $f\colon X \longrightarrow Y$ を $y=x^2$ と定義すると、f(1)=1、f(2)=4、f(3)=9、f(-3)=9 となります。ここで、集合 $Y$ の要素 $\{9\}$ は集合 $X$ の 2 つの要素 ${3},{-3}$ に対応付けられていますが、これも写像の定義を満たしています。また、集合 $Y$ の中には $\{16\}$ のように集合 $X$ から対応付けられない要素がありますが、これも写像の要件を満たしています。

なお、$X$ の要素に対応付けられた $Y$ の要素全体（ここでは $\{1,4,9\}$）を、$f$ の値域（range）または像（image）と呼びます。値域は終域の部分集合となります。

写像の要件を満たさないもの

写像の定義を確認すると、次のような対応は写像にならないことがわかります。

写像の特殊な形態としての全射、単射

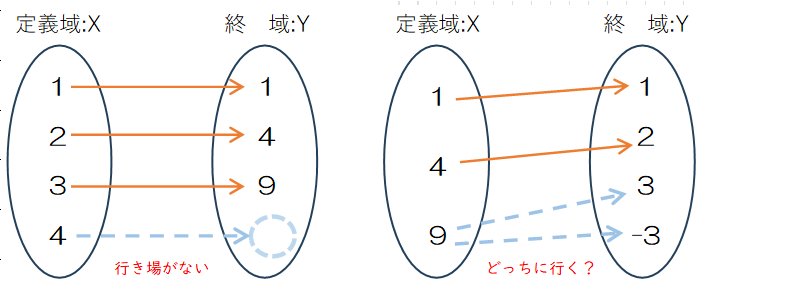
写像の中には全射、単射など、特別な性質をもつものがあります。Figure 0.3をもとに、全射と単射の概念を探っていきます。

全射

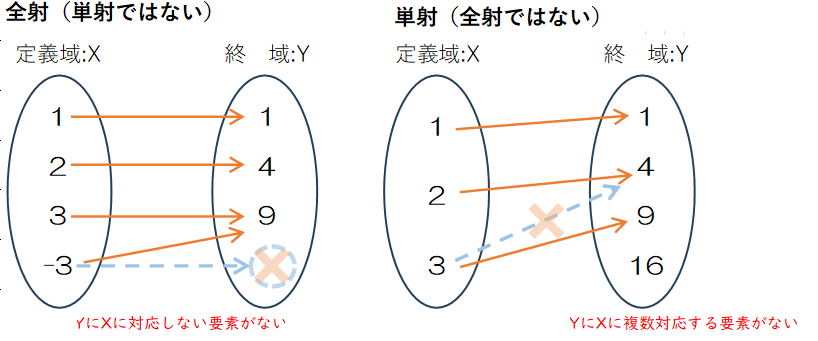
$X=\{1, 2, 3, -3\}$、$Y=\{1, 4, 9\}$と定義し、$y=x^2$ を対応させると、集合 $Y$ に集合 $X$ に対応しない要素$y$は存在しません。このように$Y$ の各要素が、必ず $X$ の少なくとも１つの要素に対応している写像を全射（surjection, surjective mapping）、または上への対応（onto mapping）と呼びます。集合 $X$ の-3と3が同じ集合 $Y$ の9に対応しますが、全射という点では問題になりません。記号で書くと次のように定義します。

$\forall y\in Y,\exists x\in X:y=f\left(x\right)$

（任意の $y$ が $Y$ に属するならば、ある $x$ が $X$ に属して $y=f(x) $を満たすものが存在する"For all y in Y, there exists an x in X such that f(x) = y）

全射では集合 $X$ 、$Y$ の要素の数を$n(X)$ 、$n(Y)$としたとき、$n(X)\geqq n(Y)$という関係が成り立ちます。

単射

$X=\{1, 2, 3\}$ 、$Y=\{1, 4, 9, 16\}$ に対し、$y=x^2$という対応を考えます。集合 $Y$ の中に集合 $X$ の2つ以上の要素から対応付けられている要素は1つもありません。このように$X$の異なる要素が、必ず $Y$の異なる要素に対応している写像を単射（injection, injective mapping）、または一対一写像（one-to-one mapping）と呼びます。なお、集合 $Y$には集合 $X$に対応しない16がありますが、単射の要件を満たしています。単射は、記号では次のように記述します。

$\forall x,x^{\prime }\in X:\left[ x\not=x^{\prime}\Rightarrow f\left(x\right)\not=f\left(x^{\prime }\right) \right] $

任意の $x$ と $x^\prime$ が $X$ に属するならば、$x$ と $x^\prime$ が等しくないならば、$f(x)$ と $f(x^\prime)$ も等しくない。

"For all x and x' in X, if x is not equal to x', then f(x) is not equal to f(x')."

集合 $X$ 、集合 $Y$ の要素の数を$n(X)$、$n(Y)$とすると、単射の場合は$n(X)\leqq n(Y)$となります。

全単射

全射と単射の両方の要件を満たす写像を全単射（bijective function, bijection）、1対1上への写像、上への1対1写像（one-to-one onto mapping）、または1対1対応（one-to-one correspondence）と呼びます。すなわち、集合$X$ の各要素が集合 $Y$ の要素1つに正確に対応するとともに、集合 $Y$ の各要素が集合 $X$ の要素1つに正確に対応するものを全単射と呼びます。

全単射は全射と単射の両方の性質を持ちます。これは、全射では $n(X) \geqq n(Y)$、単射では $n(X) \leqq n(Y)$ であるため、この両方を満たすためには $n(X) = n(Y)$ となるしかないためです。

逆写像

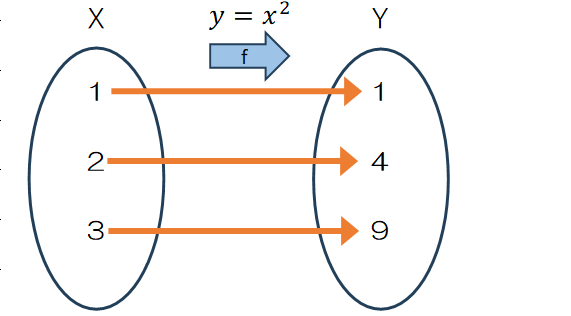
最後に、逆写像という概念をご紹介します。Figure 0.5のとおり集合 $X$ から集合 $Y$ へのという写像を考えます。

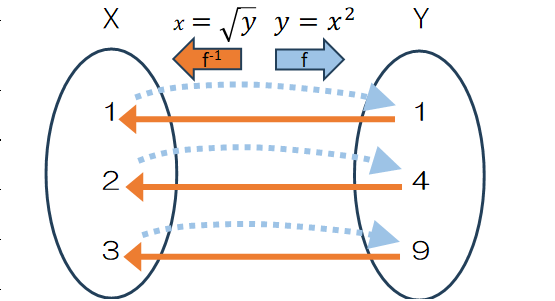
$f:X\longrightarrow Y$で$y=x^2$という対応を考えます。定義域 $X$ の各要素に対して、終域 $Y$ の要素がちょうど1つ対応しているので、この対応関係は写像の条件を満たしています。逆に、$x=\sqrt y$というyの要素からxの要素への対応を考えます。集合 $Y$ の全ての要素に対して集合 $X$ の1つの要素が対応しているので、やはり写像の要件を満たしています。このように、$f$ に対して「対応関係を逆にする写像」を逆写像（inverse mapping）と呼び、通常は $f^{-1}$ と表記します。つまり逆写像とは$y=f(x)$に対して$x=$f^{-1}(y)$となる写像をいいます。

ここで、逆写像$f^{-1}$が写像として定義できるための条件はどのようなものか考えます。

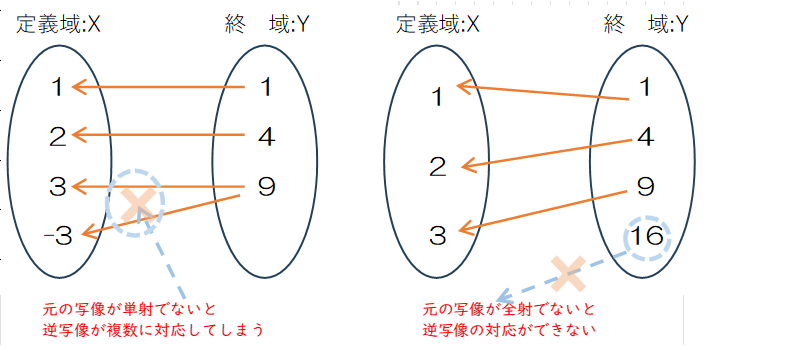
①逆写像が写像として成立するためには、単一値性（Single-valued）により集合 $Y$ の同じ要素に $X$ の複数の要素が対応することはできません。つまり、 $X$ の異なる要素が、必ず $Y$ の異なる要素に対応することになるので、写像 $f$ は単射になります。

②逆写像が写像として成立するためには、全域性（Totality）により集合 $Y$ の中に集合 $X$ と対応していない要素は存在しません。つまり、集合 $Y$ のすべての要素が、集合 $X$ の要素のどれかと対応しているので、元の写像 $f$ は全射になります。

①、②のことから、逆写像が存在する写像は、全単射であるといえます。

要素数を直接数えるのが難しい集合 $X$に対して、要素数がわかっている集合 $Y$ と全単射であることがいえれば、 $X$ の要素数を計算することができます。また、全単射であることを示すにためには、対応関係の逆写像が存在していることを証明するとうまくいくことが多くあります。

全射・単射の制限がない任意の写像

写像の条件は満たしているものの、全射の要件を満たさず集合 $Y$ に未対応の要素があったり、単射の要件を満たさず複数の $x$ が同じ $y$ に対応している写像については、広く使われている名称はありませんがテキスト内では便宜的に全射・単射の制限がない任意の写像（arbitrary mapping）と呼ぶことにします。

写像の応用

これまで写像の要件やその種類についてみてきました。この章では、それらの概念を活用し、写像が問題解決にどう役立つかについて具体例を通して見ていきます。なお、写像を組合せの分析に使う場合には、定義域を$N$、終域を$K$とすることが多いので、今後は$X$、$Y$ではなく、$N$、$K$を使用し$f:N\longrightarrow K$と表記します。

鳩の巣原理

「点の打ち方によっては $\sqrt{2}$ 以上の距離を保てるのではないか」とも「狭い領域に10個もの点を打ち込むのだから、どこかのペアは $\sqrt{2}$より近くならざるを得ないのではないか」とも思えます。いずれにしても、その納得のいく証明方法はなかなか思いつきません。このようなときに、単射の考え方が役に立ちます。

次のように正方形を3×3で9個の縦横1㎝のマスに区分けし、10個の点 $N$ から9個のマス $K$ への写像を考えます。$n(N)\geqq n(K)$から単射にはならないので、少なくとも2つの点が1つのマスに入ることになります。ところでマス内の2点の距離は、どんな工夫をしても対角線の長さ$\sqrt {2}$ より短くなります。したがって、距離が $\sqrt {2}$​ 以下となる点のペアが必ず存在します。

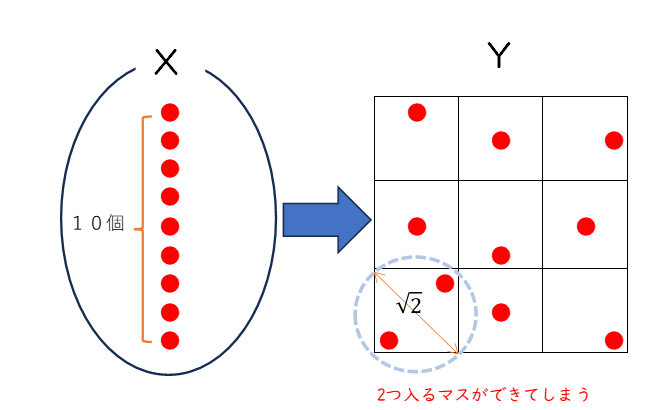
このように鳩の数が巣の数を超えると必ずあぶれる鳩が出るという、至極当然の考え方を鳩の巣原理（Pigeonhole Principle）といいます。鳩の巣原理は複雑な問題をすっきり整理するのに有効なツールになりえます。

逆写像の考え方を使うと解ける問題

逆写像による証明方法を理解するため、次の問題を考えます。

(1) 整数の分割数（partition number）またはオイラーの分割数（Euler's partition number）という有名な問題です。次の通り 11通りになります。

1+ 1+ 1+ 1+ 1+ 1

2+ 1+ 1+ 1+ 1

2+ 2+ 1+ 1

2+ 2+ 2

3+ 1+ 1+ 1

3+ 2+ 1

3+ 3

4+ 1+ 1

4+ 2

5+ 1

6

たかだか6程度の小さな整数であっても正確に数え上げるのは簡単ではありません。今後、このサイトではPythonを使って分割を生成する興味深いプログラムをご紹介します。

(2)はFigure 0.8に沿って逆写像の考え方を使い証明します。

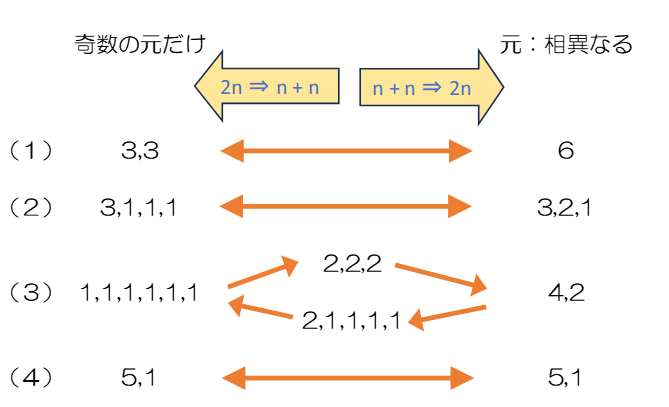
集合 $X$ を6の分割数のうち奇数の和だけで表す数として、5+ 1、3+ 3、3+ 1+ 1+ 1、1+ 1+ 1+ 1+ 1+ 1の4通りとなります。

一方、集合$Y$をすべて異なる数の和で表されるものとして 6、5+ 1、4+ 2、3+ 2+ 1の4通りとなり、確かに $n(N)=n(K)$ となります。しかし、これは6という小さな値だからたまたまそうなっただけで、もっと大きな数となると何とも言えません。どうすれば証明することができるか途方に暮れてしまいます。

そこで、次のような対応を考えます：

要素中に同じ数 $n$ があれば $2n$ に置き換える、この操作を重複がなくなるまで繰り返します。この操作では各要素の和が6であることを保ったまま同じ数字をなくしていくので、最終的には相異なる数の組合せになり、写像である要件を満たします。

偶数 $2n$ があれば、それを2で割り、その結果の中に偶数があればさらに2で割る操作を偶数がなくなるまで繰り返します。最終的には、偶数がなくなり奇数だけの組合せになります。この操作では、各要素の和が6であることを保ったまま、偶数をなくしていくので、最終的には奇数の組合せとなり、写像である要件を満たします。

よって、集合 $N$ と集合 $K$ の対応は全単射となり、$n(N) = n(K)$ になります。

確かにその通りという気もしますが、騙されたような感覚も拭えません。今後、このサイトでは、もっと大きな整数の分割でも同じルールが成り立つことを確かめていきます。

相異なる集合と区別のつかない集合

写像を使って場合の数を整理するうえで、全射や単射といった性質とは別に、もう一つ重要な視点があります。それが、「相異なる/区別のつかない」という概念です。その違いを見るために、次の問題を考えます。

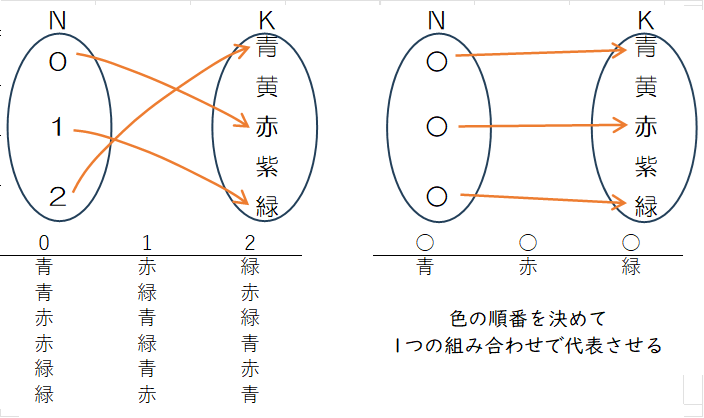
(1)は順列の例になります。集合 $N$ は$\{0, 1, 2\}$、集合 $K $について $\{青, 黄, 赤, 紫, 緑\}$　というように相異なる（distinguishable）写像になります。0,1,2がどの色を選んだかで(青、赤、緑)、(青、緑、赤)、(赤、青、緑)、(赤、緑、青)、(緑、赤、青)、(緑、青、赤)は別の順列として考えます。一方、(2)はボールつまり集合 $N$の区別のつかない写像であり、6つの順列は同じ1通りの組合せとして数えます。組合せを漏れなく、しかも重複なく生成する場合、青:0、黄:1、赤:3のように附番して、昇順に並べるのが順当なところです。このように組合せを写像で表現すると、集合$N$について区別のつかない（indistinguishable）写像となります。　

この結果、前の6つは同じ組合せとなります。例えば(青、赤、緑)がこの6つを代表します。このように、同じ単射の写像でも、定義域や終域に相異なるか否かによって、場合の数の解釈はまったく異なります。

今後、この区分は何度も登場し、プログラム名や変数にも登場します。このときdistinguishable/in distinguishableでは長すぎるので、相異なるものはdist.、区別のつかないものはindist.と略します。「相異なる/区別のつかない」は集合 $N$ と集合 $K$で独立して発生するので4通りの組合せになります。

分類の切り口と写像12相（Twelvefold way）

最終的には、対応の種類（単射、全射、写像全体）の3通の各々について、相異なる/区別のつかないという4通りがあるので計12通の写像が定義されます。

これらをまとめて分類する考え方を12通りの分類法という意味で写像12相（Twelvefold way）といいます。以下の一覧表では、12通りの分類にしたがい整理しています。