ガンマ関数は次のとおり定義されます。
$\varGamma(z)=\displaystyle\int^\infty_0e^{-t}t^{z-1}dt\quad(z>0)$
ガンマ関数にz=1/2を代入すると次のとおりガウス積分になります。
$\varGamma(1/2)=\displaystyle\int^\infty_0e^{-t}t^{-1/2}dt$
$t=s^2$とすると$dt=2sds$なので
$=\displaystyle\int^\infty_0e^{-t}t^{-1/2}dt=\int^\infty_0e^{-s^2}s^{-1}2sds$
$=\displaystyle2\int^\infty_0e^{-s^2}ds$
$e^{-s^2}=e^{-(-s)^2}$なので、次のように変換できこれはガウス積分で$a=1$のときの値になります。
$\displaystyle2\int^\infty_0e^{-s^2}ds=\int^\infty_{-\infty}e^{-s^2}ds=\sqrt{\pi}$
ガンマ関数をグラフにすると次のとおりになります。
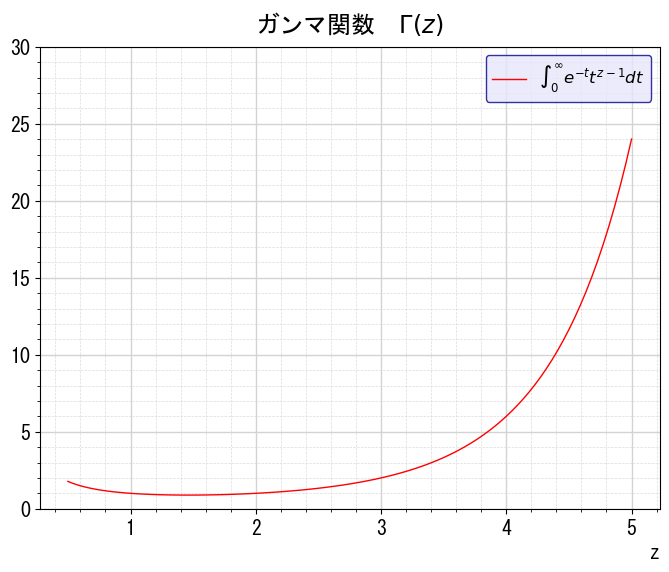
グラフをみると$\varGamma(1)=1$、$\varGamma(2)=1$、$\varGamma(3)=2$、$\varGamma(4)=6$、$\varGamma(5)=24$となります。
これだけ見ると、$\Gamma(n+1)=n!$という関係が見て取れます。このことは、$\varGamma(\alpha+1)$と$\varGamma(1)$を計算することにより導くことができます。
$\displaystyle\Gamma(\alpha+1)=\int_{0}^{\infty} t^{\alpha}e^{-t} dt$
$\displaystyle=\Bigl[-t^{\alpha}e^{-t}\Bigr]_{0}^{\infty}+\int_{0}^{\infty}\alpha t^{\alpha-1}e^{-t}dt$
$=\alpha\varGamma(\alpha)$
$\displaystyle\varGamma(1)=\int_{0}^{\infty}e^{-t}dt=\Bigl[-e^{-t}\Bigr]_{0}^{\infty}=1$
ここから前の結果が導かれます。
$\varGamma(n+1)=n\varGamma(n)=n( n-1)\varGamma(n-1)\cdots$
$=n(n-1)\cdots 2\cdot1\cdot\varGamma(1)=n!$

コメント