ガウス積分について

ガウス積分の計算とその導き方

統計学ではこんな積分が使われます。

\(\displaystyle\int^\infty_{-\infty} e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}\)

なぜ$\pi$が出てくるのか不思議です。

$I=\displaystyle \int_{-\infty}^{\infty} e^{-ax^2}dx$

$I^2=\displaystyle \left(\int_{-\infty}^{\infty} e^{-ax^2}dx\right)^2=\int_{-\infty}^{\infty}e^{-ax^2}dx \int_{-\infty}^{\infty}e^{-ay^2}dy$

$\displaystyle =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-a\left(x^2+y^2\right)}dxdy$

$x=rcos\theta\quad y=rsin\thetaとおくとx^2+y^2=r^2$

$dxdy=rdrd\theta$

$\displaystyle\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}e^{-a\left(x^2+y^2\right)}dxdy
=\int_0^{\infty}\int_0^{2\pi}e^{-ar^2}rdrd\theta\quad\cdots\;(1)$

$\displaystyle=\int_0^{2\pi}d \theta\int_0^{\infty}e^{-ar^2}rdr
=2\pi\int_0^{\infty}e^{-ar^2}rdr$

$u=r^2 とおくとdr=\frac{1}{2}du$

$\displaystyle2\pi\int_0^{\infty}e^{-ar^2}rdr=2\pi\int_0^{\infty}e^{-au}\left(\frac{1}{2}\right)du
=\pi\int_0^{\infty}e^{-au}du$

$\displaystyle=-\frac{\pi}{a}\Bigl[e^{-au}\Bigr]_0^{\infty}
=\frac{\pi}{a}$

ここで、ガウス積分が導かれました。

極座標への変換

この中で分かりずらいところは(1)の変換です。xとyを、極座標、半径：rと角度$\theta$に置き換えます。

すると、図のように$dxdy=rdrd\theta$となります。このことは次の計算式で確認できます。

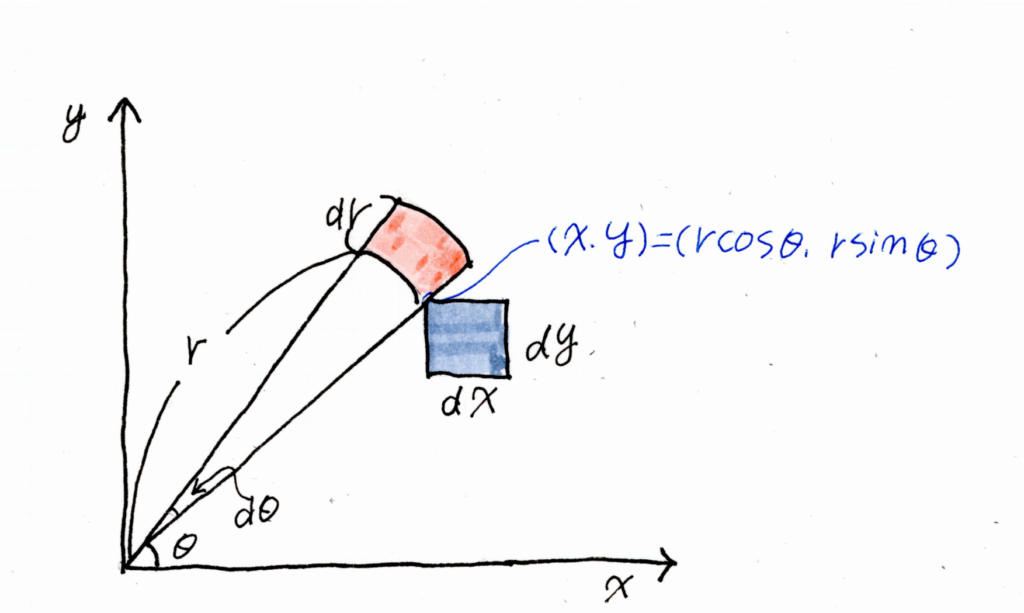
$\displaystyle dS=\pi(r+dr)^2 \times \frac{d\theta}{2 \pi}-\pi r^2 \times \frac{d\theta}{2 \pi}$

$\displaystyle =\left[(r+dr)^2-r^2\right] \times \frac{d\theta}{2}$

$\displaystyle =\left[2rdr+dr^2\right]\frac{\mathrm{d}\theta}{2}$

$\displaystyle =rdrd\theta+\frac{1}{2}dr^2d\theta$

$\frac{1}{2}dr^2d\theta$は無視できるほど小さくなるので、$dS=dxdy=rdrd\theta$となることがわかります。

もう少し格調高くヤコビアンを使っても計算できます。

$\frac{\partial x}{\partial r}=\cos\theta\hspace{5pt}\frac{\partial x}{\partial \theta}=-r \sin \theta$

$\frac{\partial y}{\partial r}=\sin \theta\hspace{5pt}\frac{\partial y}{\partial \theta}=r \cos \theta$

$x, y$ の $r, \theta$ に関するヤコビアンは

$\begin{eqnarray}\frac{\partial(x, y)}{\partial(r, \theta)}=\operatorname{det}\begin{pmatrix}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}
\end{pmatrix}\end{eqnarray}$

$\begin{eqnarray} =\operatorname{ det } \begin{pmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{pmatrix} \end{eqnarray}$

$=rcos^2\theta-(-rsin^2\theta)=r$