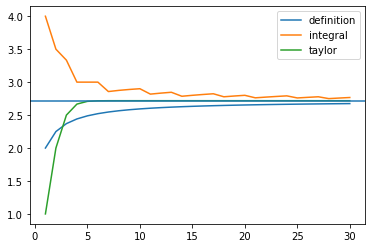
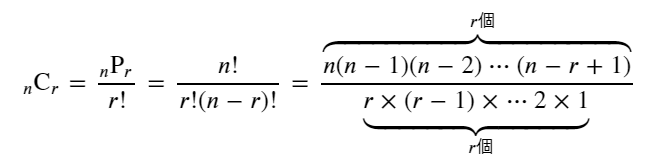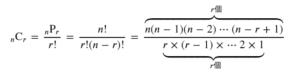順列・組み合わせの公式集

順列・組み合わせ

重複順列 (sequence with repetition)

r人をn個の部屋に分ける

$_{n}\Pi_{r}=\underbrace{n\times{n}\times\times{n}}_{r個の積}=n^r$

順列の個数(permutation)

$1\leqq x_1\ne x_2\ne\cdots \ne x_k \leqq n$

$\displaystyle {}_n\mathrm{P}_r = \frac{n!}{(n-r)!}=\overbrace {n(n-1)(n-2)・・・(n-r+1) \quad}^{r個}$

$\displaystyle {}_n\mathrm{P}_r = \frac{n!}{(n-r)!}=\overbrace {n(n-1)(n-2)・・・(n-r+1) \quad}^{r個}$

$1\le x_i\le n,1\le x_j\le n,k_i\ne k_j,1\le i\lt j \le k$

$\displaystyle {}_n\mathrm{P}_r = n(n-1)(n-2)・・・(n-r+1)=\frac{n!}{(n-r)!}$