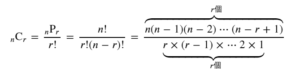きますが、k=pqが合成数の時には、$2^k – 1 = 2^{pq} – 1$ =$ (2^p-1)(2^{pq -p}+\cdots+2^{3p}+2^{2p}+2^p+1)$となり、
メルセンヌ素数に$2^{k-1}$を掛けた値が完全数になるのは次の計算ができるためです。
整数nが完全数であるため
nの約数の合計:SとするとS=2n
$M_{p}=2^{p-1}-1$、n=$M_{p}2^{p-1}$、nの約数の合計をSとすると
$n=M_{p}\cdot 2^{p-1}=(2^p-1)2^{p-1}$
$S=((2^p-1)^0+(2^p-1)^1)(2^0+2^1+2^2+\cdots+2^{p-1})$
初項1、公比 $2^p-1$ 初項1、公比2の等比数列
$=(1+2^p-1)(2^0+2^1+2^2+\cdots+2^{p-1})$
$=2^p(2^p-1)=2\cdot(2^p-1)2^{p-1}=2n$