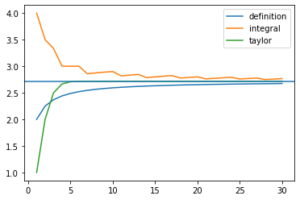
自然対数
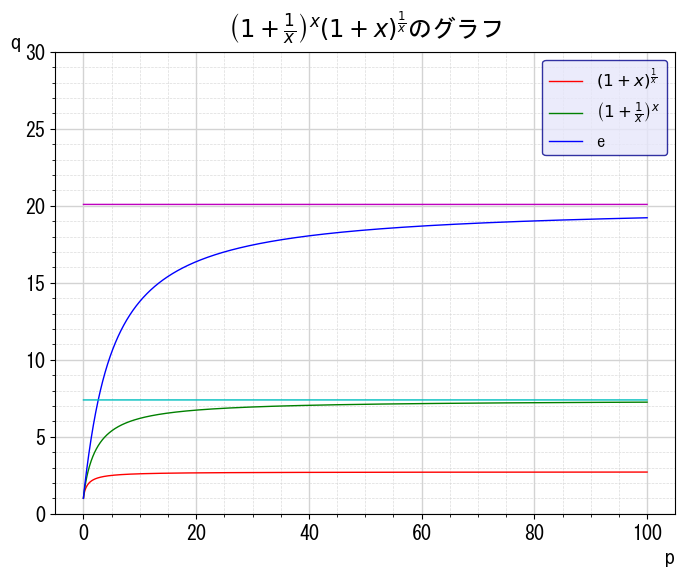
$\displaystyle e = \lim_{x\to \infty} \left(1+\frac{1}{x} \right)^{x}\sim2.718281828459045$
「鮒、一鉢二鉢一鉢二鉢至極美味しい」という語呂合わせがあります。
マイナスの無限大について
$t=-xとおくと$
$\displaystyle\lim_{x \rightarrow-\infty}\left(1+\frac{1}{x}\right)^x=\lim_{t \rightarrow \infty}\left(1-\frac{1}{t}\right)^{-t}=\lim_{t \rightarrow \infty}\left(\frac{t}{t-1}\right)^t=\displaystyle\lim_{t \rightarrow \infty}\left(1+\frac{1}{t-1}\right)^{t-1}\left(1+\frac{1}{t-1}\right)=e\quad\left(t=-x\right)$
$\therefore\displaystyle e=\lim_{x\to \pm\infty}\left(1+\frac{1}{x}\right)^{x}$
$\frac{1}{x}=t$とおくと、$x\to\pm\infty$ならば、${t\to 0}$なので、
$\displaystyle \lim_{x \to 0} (1+x)^{\frac{1}{x}}= \lim_{t\to \pm\infty} \left(1+\frac{1}{t}\right)^{t}=e$
$\displaystyle e=\lim_{x \to 0} (1+x)^{\frac{1}{x}}$とあらわすことができます。
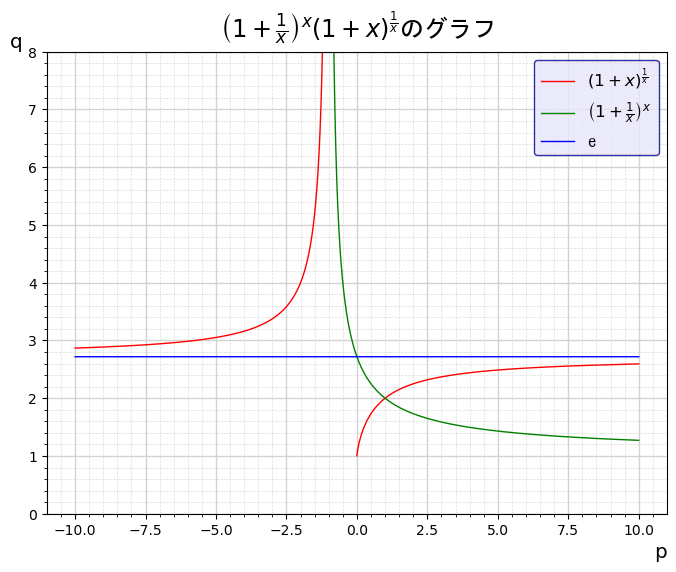
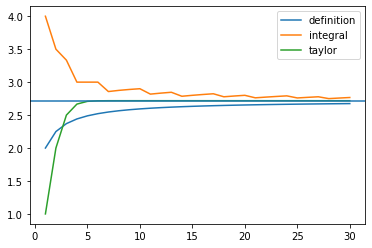
ネイピア数は次の通りあらわすことができました。
$\displaystyle e = \lim_{x\to \pm\infty} \left(1+\frac{1}{x} \right)^{x}$
ここで$\displaystyle\frac{1}{x}$を$\displaystyle\frac{a}{x}$にすると、次のとおり変形することができます。
$\displaystyle\lim_{x\to \pm\infty}\left(1+\frac{a}{x} \right)^{x}=e^a $
なぜなら、$\displaystyle \frac{x}{a}=t(a\ne0)$とおくと、$x=at$だから、$\displaystyle\lim_{x\to \pm\infty} \left(1+\frac{a}{x} \right)^{x}=\lim_{t\to \pm\infty} \left(1+\frac{a}{at} \right)^{at}=\lim_{t\to \pm\infty} \left(\left(1+\frac{1}{t} \right)^{t}\right)^a=e^a$
$a=0$なら、$\displaystyle\lim_{x\to \pm\infty} \left(1+\frac{a}{x} \right)^{x}=1^0=1,=e^0=1$となり正しくなります。早速グラフにすると計算結果が正しいことがわかります。
$\displaystyle \frac{x}{a}=t(a\ne0)$とおくと、$x=at$だから、 $\displaystyle\lim_{x\to0}(1+ax)^{\frac{1}{x}}=\lim_{t\to0}(1+t)^{\frac{a}{t}}=\lim_{t\to0}\left((1+t)^{\frac{1}{t}}\right)^a=e^a$