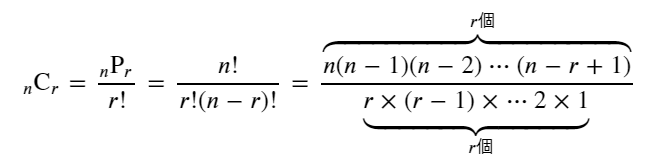ictsr4– Author –

順列・組み合わせ 重複順列 r人をn個の部屋に分ける $_{n}\Pi_{r}=\underbrace{n\times{n}\times\cdots\times{n}}_{r個の積}=n^r$ 順列 $1\le x_i\le n,1\le x_j\le n,k_i\ne k_j,1\le i\lt j \le k$ $\displaystyle {}_n\mathrm{P}_r = \frac{n!}{(n-r)!}...

順列・組み合わせ 重複順列 (sequence with repetition) r人をn個の部屋に分ける $_{n}\Pi_{r}=\underbrace{n\times{n}\times\times{n}}_{r個の積}=n^r$ 順列の個数(permutation) $1\leqq x_1\ne x_2\ne\cdots \ne x_k \leqq n$ $\displaystyle {}_n\mathr...

きますが、k=pqが合成数の時には、$2^k - 1 = 2^{pq} - 1$ =$ (2^p-1)(2^{pq -p}+\cdots+2^{3p}+2^{2p}+2^p+1)$となり、 メルセンヌ素数に$2^{k-1}$を掛けた値が完全数になるのは次の計算ができるためです。 整数nが完全数であるため nの約数の合計:Sとす...

Pythonでオイラー関数を計算する オイラー関数は、ある整数に対し、その整数より小さくかつ互いに素（最大公約数=1)となる整数の個数を計算します。オイラー関数の前提として、Pythonでは次の通り最大公約数を計算することができます。 #最大公約数を計算...

Pythonで小数型の数値を2進数に変換するために関数を作ってきましたが、この結果が本当に正しいかは全くわかりません。そこで、小数を2進数に変換する関数やメソッドを探してみましたが現時点で見つかっていません。そのかわり、16進数に変換すること、次...

Pythonで浮動小数点の計算をしていて、桁あふれの処理をするとき、あふれたbitを丸める必要があります。このときに丸める方法ための関数を作成します。このことにより、本当に細かい話ですが小数点以下のおかしな振る舞いがなぜ起ってしまうのかがわかりま...

arctanのほかにも、バーゼル問題やさらには素数から円周率を計算する方法があります。 $\displaystyle \displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^{2}}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}\cdots=\frac{\pi^2}...