SymPyで数式の大小を比較する

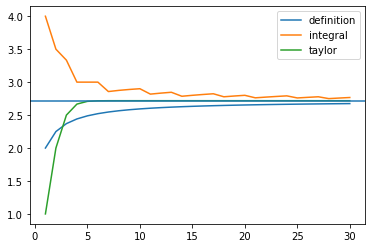
SymPyでは数式に関しても大小の比較をしてくれますが、細かく見ていくとかなり配慮が必要です。

数式に値を代入して、数字として大小を比較する

SymPyで変数を定義し、変数に具体的な数値を代入した後、その計算結果を比較します。比較にはEq関数を使います。Eq関数のEは大文字から始まります。このように、SymPyでは関数名の1文字目に大文字を使うことが多くあります。

sympy.var('x y')
x = 2
y = 4
display(sympy.Eq(2*y, 2*x+4))
display(sympy.Eq(2*y, 2*x+5))
display(sympy.Eq(2*y, 2*x+5, evaluate=False))

True 
False
8=9

SymPyでは、変数に数値を代入した場合、Eq関数でその計算結果をもとに等しいかどうかを比較することができます。4行目は2y=8、2x+4=8となり等しくなるのでTrue（等しい）と判断されます。一方、5行目は誤っているのでFalseと判断されます。ただし6行目のようにevaluate=Falseを指定すると、計算結果が示され等しいかどうかの判断はしなくなります。

次に、具体的な数値ではなくyとxの関係を示した場合の計算です。

sympy.var('x y')
y = x+2
display(sympy.Eq(2*y, 2*x+4))
display(sympy.Eq(2*y, 2*x+5))
display(sympy.Eq(2*y, 2*x+5, evaluate=False))
display(sympy.Eq(y**2, x**2+4*x+4))
display(sympy.Eq(y**2, x**2+4*x+4, evaluate=True))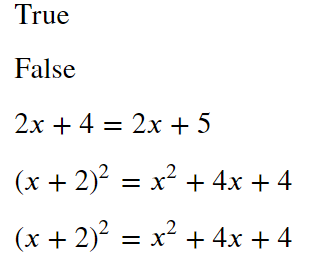

簡単な数式であると大小を判断してくれますが、複雑な数式になると数式をそのまま表示するだけになってしまいます。この場合には、symplify関数を使うと等しいかどうかの判断をしてくれます。また、yをxを使って表現したいときはrewriteメソッドを使います。

次に、xとyには数値を代入したり、関係を指定しない場合には、equalメソッドを使うと正しい（恒等式）かそうでないか判断してくれます。

expr1=(x+y)*2
expr2=x*2+2*y
expr1=(x+y)**2
expr2=x**2+2*x*y+y**2
expr1.equals(expr2)

True

この場合、恒等式となる常に等しいくなるのでTrueと判断されます。一方、必ずしも等しくない場合には次のようになります。

sympy.var('a1,a2,b1,b2')
expr3=(a1**2+a2**2)*(b1**2+b2**2)
expr4=(a1*b1+a2*b2)**2
expr3.equals(expr4)

False

コーシーシュワルツの定理になるので、等しい場合もあるが必ずしも常に等しくなるとは限らないのでFalseになります。