Pythonでネイピア（Napier）数を計算する

Pythonでネイピア数を計算します。といってもSymPyモジュールを使えば、好きな桁数だけ計算できます。

SymPyモジュールでネイピア数を計算する

import sympy
print(sympy.E.evalf(100))

2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427

evalfに有効桁数を指定すると100桁でも1000桁でも計算してくれます。

定義通りの方法でネイピア数を計算する

高校の教科書では、ネイピア数は次の通り定義されていると思います。

$e = \displaystyle \lim_{n \to \infty} \left(1+\frac{1}{n} \right)^{n}$

そこで、nの値を引数として計算する関数を作ってみます。

def exp_definition(n):
    return (1+1/n)**n    

精度は別にして、あっけないほど簡単な関数です。

積分により計算する方法

本当はこちらの方が定義通りの方法のようです。

$\displaystyle \int^a_1 \frac{1}{x}dx=1$

このときのaがネイピア数になります。

def exp_integral(d):
    ln=0
    x=1
    while True:
        x+=1/d
        ln+=1/(x*d)
        if ln>1:
            break
    return x

x軸方向の1をd個に分割した長方形と考え、その面積lnには1/(x*d)を足しこんでいって1を少しでも超えたら計算はおしまいです。dが大きいほど精度が良くなると思われます。

テイラー(Taylor）展開による方法

テイラー(Taylor）展開による方法が有名です。

$e^x= \displaystyle\lim_{k \to \infty} \left(1+\frac{x}{k} \right)^{k}=\displaystyle\sum_{k=0}^{\infty}\dfrac{x^k}{k!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\cdots$

としてx=1を代入します。nは第何項まで計算するかを示しています。

def exp_taylor(n):
    exp=1
    factor=1
    for i in range(1,n):
        factor*=i
        exp+=1**i/factor
    return exp    

階乗の計算は、関数でもできますが、1回1回やっていると大変なので、$n!=n\times(n-1)!$の考え方で作りました。

3つの方法を比較してみます

それぞれの関数の引数を大きくすれば大きくするほど精度が上がることが予想されます。どの方法が一番小さい値で精度を出すことができるかを調べてみます。

import matplotlib.pyplot as plt
import matplotlib.style
import numpy as np
import sympy
fig ,ax = plt.subplots()

x=list(range(1,31))
definition=[]
integral =[]
taylor=[]
for i in x: 
    definition.append(exp_definition(i))
    integral.append(exp_integral (i))
    taylor.append(exp_taylor(i))
    
plt.plot(x, definition,label='definition')
plt.plot(x, integral,label='integral ')
plt.plot(x, taylor,label='taylor')
ax.axhline(sympy.E)
ax.legend()
plt.plot
plt.show()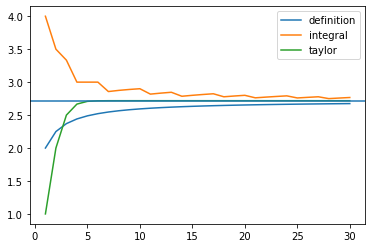

それぞれ意味するところが異なるので一概に比較するのもどうかと思いますが、テイラー展開の場合にはかなり早く良い数字になっていきます。一方、積分による方法もちろん10回程度で良い数にになりますが、きれいな曲線にならないところが興味を惹かれます。