Pythonで円周率を計算する～最も素朴な方法

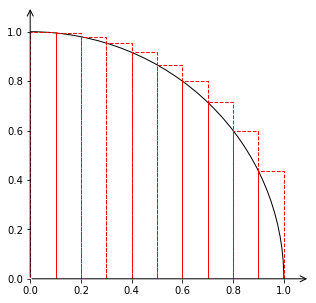
円周率を計算するのに、とりあえず頭に浮かぶ最も素朴な方法で計算します。まず、半径1の4分円の面積を求めるます。$x$の範囲である0から1を10等分し、0.0から0.9までの値を考えます。それぞれについて円の方程式から、yの値を計算します。

円の方程式　$x^2+y^2=1$ ==> $\displaystyle y=\sqrt{\mathstrut 1-x^2}$

この数式にx=0.0からx=0.9まで計算し、その総和が半径1の4分円の面積に近似するという考え方です。

square=0
d=10
for i in range (d):
    y=(1-(i/d)**2)**0.5
    square+=y
square/d*4

#3.160417031779045

ちなみに円周率をSymPyモジュールで有効桁数100桁まで計算すると次の通りです。

import sympy
z=sympy.pi.evalf(100)
print(z)

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068

このように、小数点第1位までは正しく計算されますが、それより小さい桁数まで見ると約0.02だけ大きめに出てしまいます。そこで、上記のプログラムを関数として、分割する数を100,1000,10000,100000と増やしていきます。

def pi1(d):
    square=0
    for  x in range (d):
        y=(1-(x/d)**2)**0.5
        square+=y
    return square/d*4

l=[100,1000,10000]
for i in l: 
    print(pi1(i))

3.160417031779045
3.143555466911023
3.1417914776113207
3.1416126164020075

分割する数を100000まで増やしても、小数点第3位までしか正しく計算することができません。そこで、関数を次のように変更します。今度は、10に分割した四角形を台形として考えます。

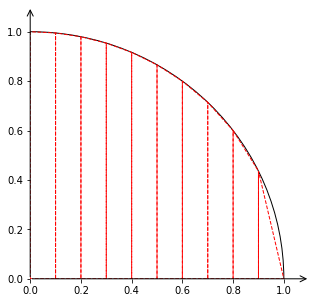
def pi2(d):
    square=0
    prev=1
    for i in range (1,d+1):
        y=(1-(i/d)**2)**0.5
        square+=(prev+y)/2
        prev=y
    return square/d*4

l=[100,1000,10000,100000]
for i in l: 
    print(pi2(i))

3.1404170317790454
3.1415554669110333
3.1415914776113127
3.1415926164019514

上記の通り、小数点第7位まで正しく計算することが可能となります。

両者の違いを見るため、xを100から1000まで100単位で変化させて円周率を計算し、グラフにしてみます。

import matplotlib.pyplot as plt
import matplotlib.style
import numpy as np
import math
fig ,ax = plt.subplots()

x=list(range(100,1001,100))
y1=[]
y2=[]
for i in x: 
    y1.append(pi1(i))
    y2.append(pi2(i))
plt.plot(x, y1)
plt.plot(x, y2)
ax.axhline(math.pi)
plt.plot
plt.show()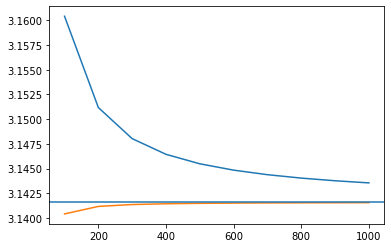

このように、2つ目の方法はかなり良い感じになります。