三角形の3つの座標が与えられたとき、その三角形の内心を求めてみます。
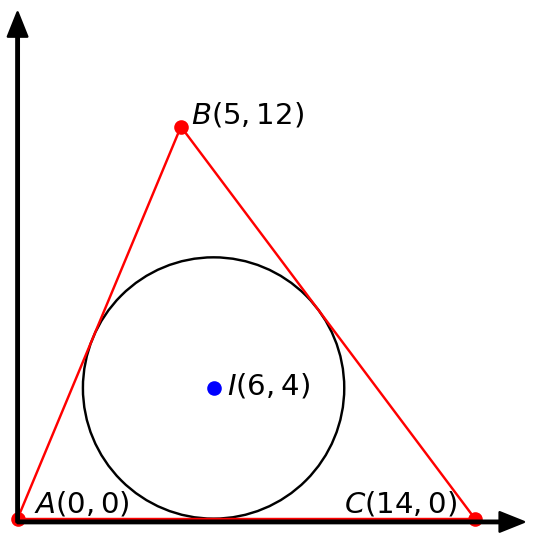
図のように、A(0,0)、B(5,12)、C(14,0)とすると、sympy.geometryモジュールを使って計算します。
import sympy.geometry
A, B, C = sympy.geometry.Point(0, 0), sympy.geometry.Point(14, 0), sympy.geometry.Point(5, 12)
tri = sympy.geometry.Triangle(A, B, C)
print('内心 = ',tri.incenter)
print('半径 = ',tri.inradius)内心 = Point2D(6, 4)
半径 = 4このように、内心I=(6,4)、半径=4であることが分かりました。これをNumPyを使って計算します。一般的には、内心は次の式で計算することができます。
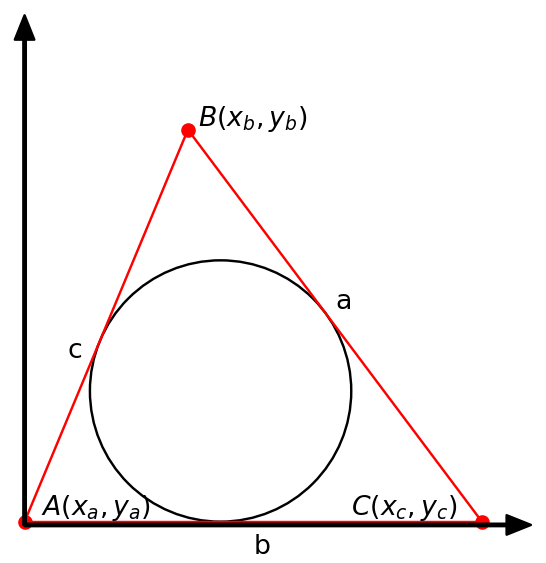
$\displaystyle \left( \frac{a x_{a} + b x_{b} + c x_{c}}{a + b + c}, \ \frac{a y_{a} + b y_{b} + c y_{c}}{a + b + c}\right)$
また、半径についてはヘロンの公式から計算することができます。式をNumPyで計算してみます。
import numpy as np
A=np.array([0,0])
B=np.array([14,0])
C=np.array([5,12])
a=np.sqrt(sum((C-B)**2))
b=np.sqrt(sum((C-A)**2))
c=np.sqrt(sum((B-A)**2))
i=(a*A+b*B+c*C)/(a+b+c)
print(i)
s=(a+b+c)/2
r=np.sqrt((s-a)*(s-b)*(s-c)/s)
print(r)[6. 4.]
4.0こんなに少ないコードで計算できるところがNumPyの素晴らしいところです。