SymPyを使うと三角関数の倍角、半角の定理の計算もすることができますが、ここまでくるとかなり工夫が必要です。
倍角定理
まずは、sinの倍角、3倍角だけでなく、4,5倍まで計算してみます。SYmPyのexpand関数でtrig=True付きで計算することができます。
double=sympy.sin(alpha*2)
display(sympy.Eq(double,sympy.expand(double,trig=True)))
triple=sympy.sin(alpha*3)
display(sympy.Eq(triple,sympy.expand(triple,trig=True)))
forth=sympy.sin(alpha*4)
display(sympy.Eq(forth,sympy.expand(forth,trig=True)))
fifth=sympy.sin(alpha*5)
display(sympy.Eq(fifth,sympy.expand(fifth,trig=True)))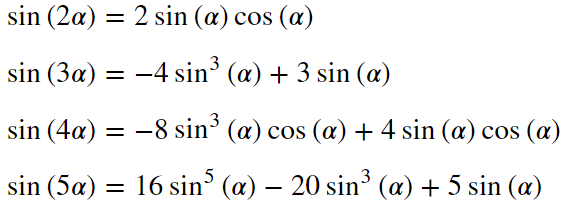
cosも同様に5倍角まで計算します。
double=sympy.cos(alpha*2)
display(sympy.Eq(double,sympy.expand(double,trig=True)))
triple=sympy.cos(alpha*3)
display(sympy.Eq(triple,sympy.expand(triple,trig=True)))
forth=sympy.cos(alpha*4)
display(sympy.Eq(forth,sympy.expand(forth,trig=True)))
fifth=sympy.cos(alpha*5)
display(sympy.Eq(fifth,sympy.expand(fifth,trig=True)))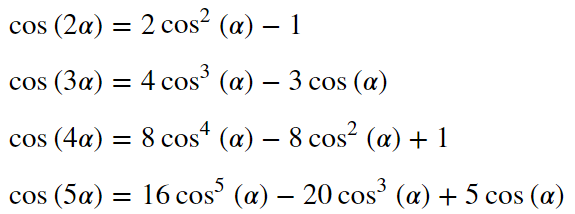
3倍角までは参考書などを見ればわかりますが、4倍角、5倍角は本当にあっているかわかりません。そこで、一応$\alpha=\pi/5$として、計算してみました。
sx=sympy.sin(sympy.pi/5)
cx=sympy.cos(sympy.pi/5)
print('正しい sin(4/5pi)=',float(sympy.sin(sympy.pi/5*4)))
print('計算式 sin(4/5pi)=',float(-8*sx**3*cx+4*sx*cx))
print('正しい sin(5/5pi)=',float(sympy.sin(sympy.pi/5*5)))
print('計算式 sin(5/5pi)=',float(16*sx**5-20*sx**3+5*sx))
print('正しい cos(4/5pi)=',float(sympy.cos(sympy.pi/5*4)))
print('計算式 cos(4/5pi)=',float(8*cx**4-8*cx**2+1))
print('正しい cos(5/5pi)=',float(sympy.cos(sympy.pi/5*5)))
print('計算式 cos(4/5pi)=',float(16*cx**5-20*cx**3+5*cx))
計算式 sin(5/5pi)= 9.454570104612593e-125は、ほぼ0なので正解とします。
半角公式
半角公式は結果が2乗となるのでなかなかむつかしいです。
halfs2=sympy.sin(alpha/2)**2
display(sympy.expand(halfs2,trig=True))
display(sympy.trigsimp(sympy.expand(halfs2,trig=True)))
import sympy.simplify.trigsimp
何をやってもダメなときはtrigsimp_groebner関数を使います。
import sympy.simplify.trigsimp
display(trigsimp_groebner(sympy.expand(halfs2,trig=True), hints=[1]))
display(trigsimp_groebner(sympy.expand(halfs2,trig=True), hints=[2]))
display(trigsimp_groebner(sympy.expand(halfs2,trig=True), hints=[3]))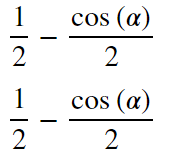
cosも同じくtrigsimp_groebner関数で計算することができます。
halfc2=sympy.cos(alpha/2)**2
display(trigsimp_groebner(sympy.expand(halfc2,trig=True), hints=[2]))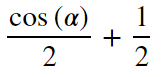
正しく計算できています。