SymPyで三角関数の演算の公式を確認します。
三角関数の加算
sinの角の加算の計算をします。expandは式の展開をしますが、そのときtrig=Trueと指定することにより、加算公式の計算をすることができます。
import sympy
sympy.var('alpha beta')
sp=sympy.sin(alpha+ beta)
display(sympy.Eq(sp,sympy.expand(sp,trig=True)))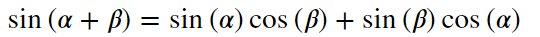
同様にcos、tanについても計算します。cosは正しく計算できますが、tanについては、もう少し簡単にしたくなります。
cp=sympy.cos(alpha+ beta)
display(sympy.Eq(cp,sympy.expand(cp,trig=True)))
tp=sympy.tan(alpha+ beta)
display(sympy.Eq(tp,sympy.expand(tp,trig=True)))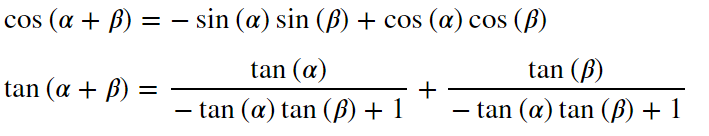
式を簡単にするためにはtrigsimp関数を使います。SymPyでは式を簡潔化するためにはsimplify関数を使いますが、これを三角関数に特化したものがtrigsimp関数です。
display(sympy.Eq(tp,sympy.simplify((sympy.expand(tp,trig=True)))))
display(sympy.Eq(tp,sympy.trigsimp((sympy.expand(tp,trig=True)))))

加法定理の逆の計算
今後は、加法定理の逆、元に戻す計算をしてみます。
se=(sympy.sin(alpha)*sympy.cos(beta)) + (sympy.sin(beta)*sympy.cos(alpha))
display(sympy.Eq(se,sympy.trigsimp((sympy.factor(se)))))
display(sympy.Eq(se,sympy.trigsimp((sympy.expand(se,trig=True)))))
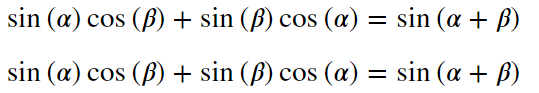
SymPyでは式の因数分解はfactor関数を使います。ただ、三角関数なので、ただの因数分解ではうまくいかず、やはりtrigsimp関数を使う必要があります。また、expand関数でもtrig=Trueを入れると、SymPyはこちらの意図を慮ってしっかりと計算してくれます。
ce=(sympy.cos(alpha)*sympy.cos(beta)) - (sympy.sin(beta)*sympy.sin(alpha))
display(sympy.Eq(se,sympy.trigsimp((sympy.factor(ce)))))
display(sympy.Eq(ce,sympy.trigsimp((sympy.expand(ce,trig=True)))))
te=(sympy.tan(alpha)+sympy.tan(beta))/(1-(sympy.tan(alpha)*sympy.tan(beta)))
display(sympy.Eq(te,sympy.trigsimp((sympy.factor(te)))))
display(sympy.Eq(te,sympy.trigsimp((sympy.expand(te,trig=True)))))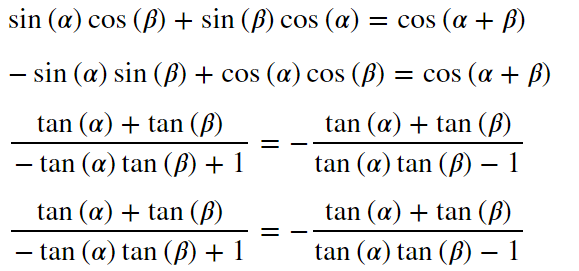
cosまではしっかりと計算してくれますが、tanまでいくとむつかしいようです。