$\displaystyle\int_{-\infty}^{\infty}\exp(\alpha x-e^{x})dx$
を$x=\log\alpha$ の近傍でテイラー展開しました。なぜ$x=\log\alpha$なのでしょうか。
expの中身を$f(x)$とすると
$f(x)=\alpha x-e^{x} \quad(\alpha\gt0)$
$f'(x)=\alpha-e^{x}=0$とおくと
$\alpha=e^{x}$から$x=\log\alpha$
$f(x)はグラフの通り、x=\log\alpha$の付近で最大となり、そこから$x$が増えても減っても急速に減少します。
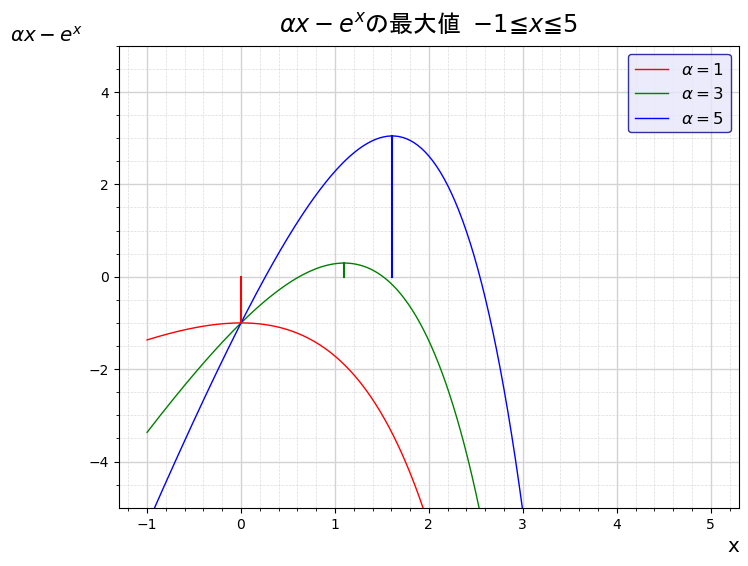
さらに最終的には$\exp(\alpha-e^{x})$の積分を考えると、次のとおり$x=\log\alpha$の近傍が積分の値に最も影響を充てると考えられるためです。

また、上記ブログの(2)の部分も気になります。なぜ、次のような変換ができるのでしょうか。
$\displaystyle\varGamma(\alpha)\sim\Bigl(\frac{\alpha}{e}\Bigr)^{\alpha} \int_{-\infty}^{\infty}\exp\Bigl(-\frac{\alpha}{2}(x-\log\alpha )^{2}\Bigr)dx$
$\displaystyle=\Bigl(\frac{\alpha}{e}\Bigr)^{\alpha}\int_{-\infty}^{\infty}\exp\Bigl(-\frac{\alpha}{2}x^{2}\Bigr)dx$
2つの被積分関数を比べてグラフにすると次の通りになります。
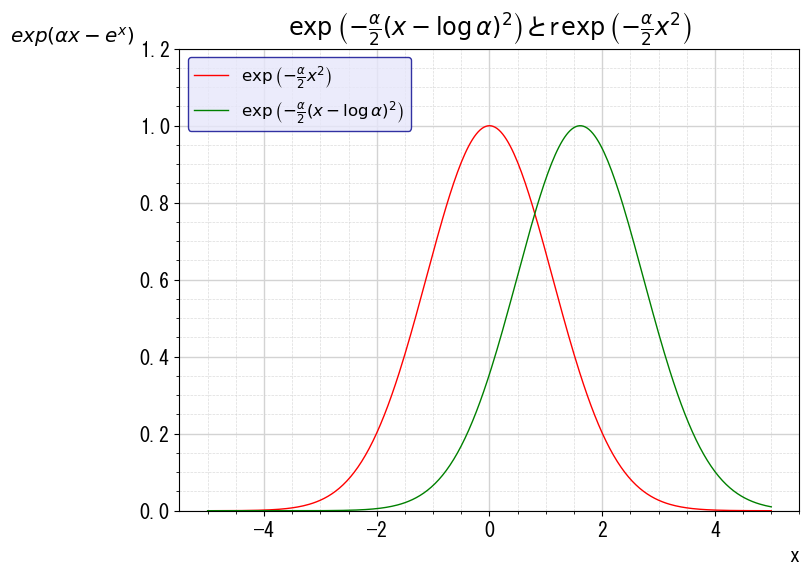
ということで、2つの式の積分値を無条件に等しいとはできませんが、マイナス無限大から無限大で積分する分には等しくなりそうです。比べると次のようになります。
for alpha in range(1,10):
func1 = integrate.quad(lambda x_ar:np.exp((-2/alpha)*x_ar**2),-np.inf, np.inf)[0]
func2 = integrate.quad(lambda x_ar:np.exp((-2/alpha)*(x_ar-np.log(alpha))**2),-np.inf, np.inf)[0]
print(f'{alpha:2d}{func1:>16.12f}{func2:>16.12f}') 1 1.253314137316 1.253314137316
2 1.772453850906 1.772453850906
3 2.170803763675 2.170803763675
4 2.506628274631 2.506628274631
5 2.802495608199 2.802495608199
6 3.069980123839 3.069980123839
7 3.315957521978 3.315957521978
8 3.544907701811 3.544907701811
9 3.759942411947 3.759942411947

コメント