ガンマ関数の漸近展開での積分について

ガンマ関数の漸近展開で、次の計算をしました。

$\displaystyle\varGamma(\alpha+1)=\int_{0}^{\infty} t^{\alpha}e^{-t}dt$

$\displaystyle=\Bigl[-t^{\alpha}e^{-t}\Bigr]_{0}^{\infty}\quad\cdots\;(1)$

$\displaystyle=+\int_{0}^{\infty}\alpha t^{\alpha-1}e^{-t}dt$

$=\alpha\varGamma(\alpha)$

ここで(1)の部分が0になるというのは、次の式から導くことができます。

$\displaystyle\lim_{x\to 0}-t^{\alpha}e^{-t}=0$

$\displaystyle\lim_{x\to\infty}-t^{\alpha}e^{-t}=0$

もう少し直感的に捉えるためにグラフにしてみます。

$\alpha=1,3,5$について、$0\leqq t\leqq2$の区間をグラフを描いてみます。

このことから$\alpha$の値によらず、$t=0$のとき関数の値は0になります。一方、$0\leqq t\leqq20$の区間だと次のようになります。

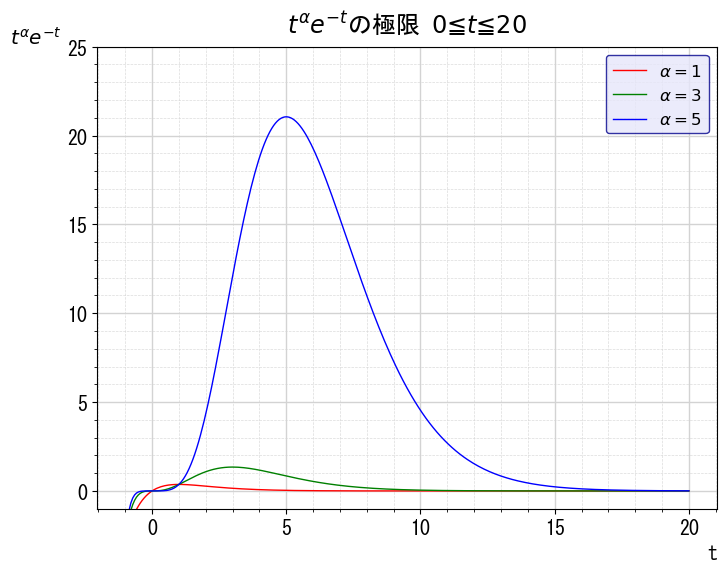
このように$\alpha$の値により多少差はありますが、ある程度$t$が大きくなると関数の値は0に収束することが見て取れます。

pythonを使うと次にように簡単なコードでグラフを描くことができます。これは本当に画期的なことです。

上記のグラフ、pythonでは次のコードで描くことができます。

t_ar = np.linspace(-1,20,301,endpoint =True)
alpha_ar = [1,3,5]
func_ar = []
label_ar = []
for alpha in alpha_ar:
    func_ar.append(t_ar**alpha*np.e**(-t_ar))
    label_ar.append(r'$\alpha='+str(alpha)+'$')
fig,ax = graph_plt(r'$t^{\alpha}e^{-t}$の極限 $0\leqq t\leqq20$',t_ar,func_ar,label_ar,x_label='t',y_label=r'$t^{\alpha}e^{-t}$',
                  y_lim=(-1, 25))
plt.show()

いろいろな$\alpha$をリストalpha_arで指定するだけでグラフ化できます。